Ego is the Enemy: The Legend of Genghis Khan
In his book, Ego is the Enemy, Ryan Holiday tells the story of Genghis Khan and how his openness to learning was the foundation of his success.
The legend of Genghis Khan has echoed through history: A barbarian conqueror, fueled by bloodlust, terrorizing the civilized world. We have him and his Mongol horde traveling across Asia and Europe, insatiable, stopping at nothing to plunder, rape, and kill not just the people who stood in their way, but the cultures they had built. Then, not unlike his nomadic band of warriors, this terrible cloud simply disappeared from history, because the Mongols built nothing that could last. Like all reactionary, emotional assessments, this could not be more wrong. For not only was Genghis Khan one of the greatest military minds who ever lived, he was a perpetual student, whose stunning victories were often the result of his ability to absorb the best technologies, practices, and innovations of each new culture his empire touched. In fact, if there is one theme in his reign and in the several centuries of dynastic rule that followed, it’s this: appropriation.
Under Genghis Khan’s direction, the Mongols were as ruthless about stealing and absorbing the best of each culture they encountered as they were about conquest itself. Though there were essentially no technological inventions, no beautiful buildings or even great Mongol art, with each battle and enemy, their culture learned and absorbed something new. Genghis Khan was not born a genius. Instead, as one biographer put it, his was “a persistent cycle of pragmatic learning, experimental adaptation, and constant revision driven by his uniquely disciplined and focused will.”
He was the greatest conqueror the world ever knew because he was more open to learning than any other conqueror has ever been.
Khan’s first powerful victories came from the reorganization of his military units, splitting his soldiers into groups of ten. This he stole from neighboring Turkic tribes, and unknowingly converted the Mongols to the decimal system. Soon enough, their expanding empire brought them into contact with another “technology” they’d never experienced before: walled cities. In the Tangut raids, Khan first learned the ins and outs of war against fortified cities and the strategies critical to laying siege, and quickly became an expert. Later, with help from Chinese engineers, he taught his soldiers how to build siege machines that could knock down city walls. In his campaigns against the Jurched, Khan learned the importance of winning hearts and minds. By working with the scholars and royal family of the lands he conquered, Khan was able to hold on to and manage these territories in ways that most empires could not. Afterward, in every country or city he held, Khan would call for the smartest astrologers, scribes, doctors, thinkers, and advisers—anyone who could aid his troops and their efforts. His troops traveled with interrogators and translators for precisely this purpose.
It was a habit that would survive his death. While the Mongols themselves seemed dedicated almost solely to the art of war, they put to good use every craftsman, merchant, scholar, entertainer, cook, and skilled worker they came in contact with. The Mongol Empire was remarkable for its religious freedoms, and most of all, for its love of ideas and convergence of cultures. It brought lemons to China for the first time, and Chinese noodles to the West. It spread Persian carpets, German mining technology, French metalworking, and Islam. The cannon, which revolutionized warfare, was said to be the resulting fusion of Chinese gunpowder, Muslim flamethrowers, and European metalwork. It was Mongol openness to learning and new ideas that brought them together.
As we first succeed, we will find ourselves in new situations, facing new problems. The freshly promoted soldier must learn the art of politics. The salesman, how to manage. The founder, how to delegate. The writer, how to edit others. The comedian, how to act. The chef turned restaurateur, how to run the other side of the house.
This is not a harmless conceit. The physicist John Wheeler, who helped develop the hydrogen bomb, once observed that “as our island of knowledge grows, so does the shore of our ignorance.” In other words, each victory and advancement that made Khan smarter also bumped him against new situations he’d never encountered before. It takes a special kind of humility to grasp that you know less, even as you know and grasp more and more. It’s remembering Socrates’ wisdom lay in the fact that he knew that he knew next to nothing.
With accomplishment comes a growing pressure to pretend that we know more than we do. To pretend we already know everything. Scientia infla (knowledge puffs up). That’s the worry and the risk—thinking that we’re set and secure, when in reality understanding and mastery is a fluid, continual process.
The nine-time Grammy– and Pulitzer Prize–winning jazz musician Wynton Marsalis once advised a promising young musician on the mind-set required in the lifelong study of music: “Humility engenders learning because it beats back the arrogance that puts blinders on. It leaves you open for truths to reveal themselves. You don’t stand in your own way. . . . Do you know how you can tell when someone is truly humble? I believe there’s one simple test: because they consistently observe and listen, the humble improve. They don’t assume, ‘I know the way.’”
No matter what you’ve done up to this point, you better still be a student. If you’re not still learning, you’re already dying.
It is not enough only to be a student at the beginning. It is a position that one has to assume for life. Learn from everyone and everything. From the people you beat, and the people who beat you, from the people you dislike, even from your supposed enemies. At every step and every juncture in life, there is the opportunity to learn—and even if the lesson is purely remedial, we must not let ego block us from hearing it again.
Too often, convinced of our own intelligence, we stay in a comfort zone that ensures that we never feel stupid (and are never challenged to learn or reconsider what we know). It obscures from view various weaknesses in our understanding, until eventually it’s too late to change course. This is where the silent toll is taken.
Each of us faces a threat as we pursue our craft. Like sirens on the rocks, ego sings a soothing, validating song— which can lead to a wreck. The second we let the ego tell us we have graduated, learning grinds to a halt. That’s why Frank Shamrock said, “Always stay a student.” As in, it never ends.
The solution is as straightforward as it is initially uncomfortable: Pick up a book on a topic you know next to nothing about. Put yourself in rooms where you’re the least knowledgeable person. That uncomfortable feeling, that defensiveness that you feel when your most deeply held assumptions are challenged—what about subjecting yourself to it deliberately? Change your mind. Change your surroundings
An amateur is defensive. The professional finds learning (and even, occasionally, being shown up) to be enjoyable; they like being challenged and humbled, and engage in education as an ongoing and endless process.
Most military cultures—and people in general—seek to impose values and control over what they encounter. What made the Mongols different was their ability to weigh each situation objectively, and if need be, swap out previous practices for new ones. All great businesses start this way, but then something happens. Take the theory of disruption, which posits that at some point in time, every industry will be disrupted by some trend or innovation that, despite all the resources in the world, the incumbent interests will be incapable of responding to. Why is this? Why can’t businesses change and adapt?
A large part of it is because they lost the ability to learn. They stopped being students. The second this happens to you, your knowledge becomes fragile.
The great manager and business thinker Peter Drucker says that it’s not enough simply to want to learn. As people progress, they must also understand how they learn and then set up processes to facilitate this continual education. Otherwise, we are dooming ourselves to a sort of self-imposed ignorance.
https://fs.blog/ego-is-the-enemy-genghis-khan/
Concept of Knowledge Revisited
Imam al-Mu’izz: “… I find no greater bliss, comfort and yearning than in seeking knowledge”
Posted by Nimira Dewji
The Tayyibi Ismaili scholar and author Idris Imad al-Din (d. 1468 CE) was the chief da’i of the Yemeni Ismaili da’wa, descended from the prominent al-Walid family, who led the Tayyibi Musta‘lian Ismaili administration for more than three centuries. Thus, Idris had access to the literary heritage of the Ismailis, including the majority of the surviving Fatimid texts.
In his seven-volume Uyun al-akhbar wa funun al-athar (‘Sound Sources and Trustworthy Traditions‘), composed around 1434, Idris recounts the key developments in Ismaili history from the time of Prophet Muhammad and the Shi’i Ismaili Imams until the decline of the Fatimid dynasty in the twelfth century. The text draws upon the sayings and anecdotes of Imam al-Mu’izz as recounted by his chief judge and chief da’i al-Qadi al-Nu’man (d. 974).
“The works of al-Nu’man are among the earliest Fatimid writings on the history and doctrines of the Ismaili imams, as well as the authoritative source on al-Mu’izz’s words and actions. Idris’s extensive referencing of the Qadi’s works in his narrative indicates their continued importance in Ismaili thought, long after the demise of the Fatimid state” (The Founder of Cairo p 2).
Uyun al-akhbar idris IIS muizz

Uyun al-Akhbar. Image: The Institute of Ismaili Studies
The fourth Fatimid Caliph and fourteenth Ismaili Imam al-Mu’izz (r. 953-975), succeeded his father at the age of twenty-one years. During his reign of twenty-two years, Imam al-Mu’izz reigned over the North Africa from the shores of the Atlantic to the Red Sea, conquering Egypt in 969. He came into contact with a host of regional powers, each dynasty committed to expanding its domain, causing political as well as ideological conflict, often resulting in military confrontations. “In determining his responses to these challenges as well as in venturing into diplomatic and economic interactions, al-Mu’izz had the opportunity and acumen to draw upon the experience of his three predecessors who had weathered numerous internal and external challenges in their half century of rule over the region” (The Founder of Cairo, p 10).
Imam al-Mu’izz’s quest for knowledge
“The Commander of the Faithful [al-Mu’izz] directed the matters of his da’wa and opened the gates of his knowledge and wisdom. He used to sit in person to exhort his supporters (shi’a) and followers with the lofty exhortations and instill in them learning and good action. He taught them himself and drew their young and their old close to him. The wisdom, knowledge and eloquence that he manifested was not evident in anyone else.
He was distinguished in the various types of knowledge, attaining a proficiency in some areas that even the experts lacked. Al-Qadi al-Nu’man b. Muhammad has recounted his merits, virtues and erudition which were possessed by none other than God’s proofs and awliya whom He had appointed to guide His servants, chose them for His lands, and designated them successors to the prophets and imams of the faithful.
God’s support of al-Mu’izz li-Din Allah was evident in the eloquence and knowledge that he manifested from the early years of his life and experience. People knew of no teacher to teach him or inspirer to inspire him except for the imam (wali Allah) who confided his secrets in him and made him responsible after him. He imparted the knowledge of his forefathers that they had inherited from the Messenger of God, which had been revealed in his heart by the Trustworthy Spirit (al-ruh al-amin).* Even so, he coveted knowledge, avidly seeking it, augmenting it and was eager for it.
It was reported from al-Qadi al-Nu’man, that he said:
I heard al-Mu’izz expressing what he felt by saying, ‘By God, I find no greater bliss, comfort and yearning than in seeking knowledge. If the people of this lower world were to discover this, they would renounce everything for it. If God in His Majesty had not obligated me to attend to the exoteric (zahir) matters of this world, to establish support for the people and to ensure their welfare, I would have renounced that in pursuit of knowledge and reflected over it. Nonetheless, the responsibility that I have been designated with concerning the matters of this world entails considerable knowledge for those who comprehend, and a proof for those who consider and contemplate.
Al-Qadi al-Nu’man narrated a similar report regarding Imam al-Mu’izz li-Din Allah. He said: One day while I was accompanying al-Mu’izz li-Din Allah to attend to a matter, something was mentioned concerning knowledge which had been discussed previously.
He said:
I came across something similar a few nights ago and I know a work that discusses the issue, so I sent for it. However, the one who was to bring the book did not know its location. So I went in person to the library and opened some trunks. I began searching for that work in the place where I reckoned it should be. That was in the early evening. I leafed through the books. Every time I came across a text and thumbed through it, I saw something I wished to examine. Then another text would pass my hands and the same thing would happen. I continued standing, leafing through one text after another. So engrossed was I in what I was doing that I did not think to sit down. Only when it was midnight did I become aware of my prolonged standing after I felt a sharp pain in my leg. I left, and when I awoke [the next morning] the pain was still afflicting my leg.
*In a number of sayings attributed to the Imams Muhammad al-Baqir and Ja’far al-Sadiq, the imams were said to be inspired by the ‘Holy Spirit’ (al-Ruh al-Qudus), by which they are guided, protected and granted knowledge of the unseen. In subsequent Shi’i Imami thought, the notions relating to this celestial spirit, one with Qur’anic antecedents, become integral in conceptions of the imamate” (The Founder of Cairo, p 106, n 235).
~*~*~
“The quest for knowledge is never-ending, and those with the necessary preparedness must pay close attention to the advice that God addresses to the Prophet: ‘Say: “My Lord, increase me in knowledge” (Qur’an 20:114) (Chittick, The Islamic concept of Human Perfection p 3).

Image: The Institute of Ismaili Studies
“In Islamic belief, knowledge is two-fold. There is that revealed through the Holy Prophet [Salla-llahu ‘alayhi wa- sallam] and that which man discovers by virtue of his own intellect. Nor do these two involve any contradiction, provided man remembers that his own mind is itself the creation of God. Without this humility, no balance is possible. With it, there are no barriers. Indeed one strength of Islam has always lain in its belief that creation is not static but continuous, that through scientific and other endeavours, God has opened and continues to open new windows for us to see the marvels of His creation.”
Mawlana Hazar Imam, Karachi, 16 March 1983
Speech
Sources:
The Founder of Cairo, Translated with annotations by Shainool Jiwa, I.B. Tauris, London, 2013, p 106-108
Video – Shainool Jiwa discuses The Founder of Cairo
nimirasblog.wordpress.com/2022/05/09/imam-al-muizz-i-find-no-greater-bliss-comfort-and-yearning-than-in-seeking-knowledge/
The Tayyibi Ismaili scholar and author Idris Imad al-Din (d. 1468 CE) was the chief da’i of the Yemeni Ismaili da’wa, descended from the prominent al-Walid family, who led the Tayyibi Musta‘lian Ismaili administration for more than three centuries. Thus, Idris had access to the literary heritage of the Ismailis, including the majority of the surviving Fatimid texts.
In his seven-volume Uyun al-akhbar wa funun al-athar (‘Sound Sources and Trustworthy Traditions‘), composed around 1434, Idris recounts the key developments in Ismaili history from the time of Prophet Muhammad and the Shi’i Ismaili Imams until the decline of the Fatimid dynasty in the twelfth century. The text draws upon the sayings and anecdotes of Imam al-Mu’izz as recounted by his chief judge and chief da’i al-Qadi al-Nu’man (d. 974).
“The works of al-Nu’man are among the earliest Fatimid writings on the history and doctrines of the Ismaili imams, as well as the authoritative source on al-Mu’izz’s words and actions. Idris’s extensive referencing of the Qadi’s works in his narrative indicates their continued importance in Ismaili thought, long after the demise of the Fatimid state” (The Founder of Cairo p 2).
Uyun al-akhbar idris IIS muizz

Uyun al-Akhbar. Image: The Institute of Ismaili Studies
The fourth Fatimid Caliph and fourteenth Ismaili Imam al-Mu’izz (r. 953-975), succeeded his father at the age of twenty-one years. During his reign of twenty-two years, Imam al-Mu’izz reigned over the North Africa from the shores of the Atlantic to the Red Sea, conquering Egypt in 969. He came into contact with a host of regional powers, each dynasty committed to expanding its domain, causing political as well as ideological conflict, often resulting in military confrontations. “In determining his responses to these challenges as well as in venturing into diplomatic and economic interactions, al-Mu’izz had the opportunity and acumen to draw upon the experience of his three predecessors who had weathered numerous internal and external challenges in their half century of rule over the region” (The Founder of Cairo, p 10).
Imam al-Mu’izz’s quest for knowledge
“The Commander of the Faithful [al-Mu’izz] directed the matters of his da’wa and opened the gates of his knowledge and wisdom. He used to sit in person to exhort his supporters (shi’a) and followers with the lofty exhortations and instill in them learning and good action. He taught them himself and drew their young and their old close to him. The wisdom, knowledge and eloquence that he manifested was not evident in anyone else.
He was distinguished in the various types of knowledge, attaining a proficiency in some areas that even the experts lacked. Al-Qadi al-Nu’man b. Muhammad has recounted his merits, virtues and erudition which were possessed by none other than God’s proofs and awliya whom He had appointed to guide His servants, chose them for His lands, and designated them successors to the prophets and imams of the faithful.
God’s support of al-Mu’izz li-Din Allah was evident in the eloquence and knowledge that he manifested from the early years of his life and experience. People knew of no teacher to teach him or inspirer to inspire him except for the imam (wali Allah) who confided his secrets in him and made him responsible after him. He imparted the knowledge of his forefathers that they had inherited from the Messenger of God, which had been revealed in his heart by the Trustworthy Spirit (al-ruh al-amin).* Even so, he coveted knowledge, avidly seeking it, augmenting it and was eager for it.
It was reported from al-Qadi al-Nu’man, that he said:
I heard al-Mu’izz expressing what he felt by saying, ‘By God, I find no greater bliss, comfort and yearning than in seeking knowledge. If the people of this lower world were to discover this, they would renounce everything for it. If God in His Majesty had not obligated me to attend to the exoteric (zahir) matters of this world, to establish support for the people and to ensure their welfare, I would have renounced that in pursuit of knowledge and reflected over it. Nonetheless, the responsibility that I have been designated with concerning the matters of this world entails considerable knowledge for those who comprehend, and a proof for those who consider and contemplate.
Al-Qadi al-Nu’man narrated a similar report regarding Imam al-Mu’izz li-Din Allah. He said: One day while I was accompanying al-Mu’izz li-Din Allah to attend to a matter, something was mentioned concerning knowledge which had been discussed previously.
He said:
I came across something similar a few nights ago and I know a work that discusses the issue, so I sent for it. However, the one who was to bring the book did not know its location. So I went in person to the library and opened some trunks. I began searching for that work in the place where I reckoned it should be. That was in the early evening. I leafed through the books. Every time I came across a text and thumbed through it, I saw something I wished to examine. Then another text would pass my hands and the same thing would happen. I continued standing, leafing through one text after another. So engrossed was I in what I was doing that I did not think to sit down. Only when it was midnight did I become aware of my prolonged standing after I felt a sharp pain in my leg. I left, and when I awoke [the next morning] the pain was still afflicting my leg.
*In a number of sayings attributed to the Imams Muhammad al-Baqir and Ja’far al-Sadiq, the imams were said to be inspired by the ‘Holy Spirit’ (al-Ruh al-Qudus), by which they are guided, protected and granted knowledge of the unseen. In subsequent Shi’i Imami thought, the notions relating to this celestial spirit, one with Qur’anic antecedents, become integral in conceptions of the imamate” (The Founder of Cairo, p 106, n 235).
~*~*~
“The quest for knowledge is never-ending, and those with the necessary preparedness must pay close attention to the advice that God addresses to the Prophet: ‘Say: “My Lord, increase me in knowledge” (Qur’an 20:114) (Chittick, The Islamic concept of Human Perfection p 3).

Image: The Institute of Ismaili Studies
“In Islamic belief, knowledge is two-fold. There is that revealed through the Holy Prophet [Salla-llahu ‘alayhi wa- sallam] and that which man discovers by virtue of his own intellect. Nor do these two involve any contradiction, provided man remembers that his own mind is itself the creation of God. Without this humility, no balance is possible. With it, there are no barriers. Indeed one strength of Islam has always lain in its belief that creation is not static but continuous, that through scientific and other endeavours, God has opened and continues to open new windows for us to see the marvels of His creation.”
Mawlana Hazar Imam, Karachi, 16 March 1983
Speech
Sources:
The Founder of Cairo, Translated with annotations by Shainool Jiwa, I.B. Tauris, London, 2013, p 106-108
Video – Shainool Jiwa discuses The Founder of Cairo
nimirasblog.wordpress.com/2022/05/09/imam-al-muizz-i-find-no-greater-bliss-comfort-and-yearning-than-in-seeking-knowledge/
Imaginary Numbers Are Reality
How the modern world arose from imaginary numbers.

Imaginary numbers are not imaginary at all. The truth is, they have had far more impact on our lives than anything truly imaginary ever could. Without imaginary numbers, and the vital role they played in putting electricity into homes, factories, and internet server-farms, the modern world would not exist. Students who might complain to their math teacher that there’s no point in anyone learning how to use imaginary numbers would have to put down their phone, turn off their music, and pull the wires out of their broadband router. But perhaps we should start with an explanation of what an imaginary number is.
We know by now how to square a number (multiply it by itself), and we know that negative numbers make a positive number when squared; a minus times a minus is a plus, remember? So (–2) × (–2) = 4. We also know that taking a square root is the inverse of squaring. So the possible square roots of 4 are 2 and –2. The imaginary number arises from asking what the square root of –4 would be.
What we’re discovering here is not some deep mystery about the universe.
Surely the question is meaningless? If you square a number, whether positive or negative, the answer is positive. So you can’t do the inverse operation if you start with a negative number. That’s certainly what Heron of Alexandria seemed to think. Heron was the Egyptian architect whose mathematical tricks, written in Stereometrica, gave us the dome of the Hagia Sophia. In the same volume, he showed how to calculate the volume of a truncated square pyramid; that is, a pyramid with the top chopped off. His solution for one example involved subtracting 288 from 225 and finding the square root of the result. The result, though, is a negative number: –63. So the answer would be found via √–63.
For some reason—whether a sense that there was some mistake, or someone copied something down wrong, or because it was so absurd—the manuscripts we have show that Heron ignored the minus sign and gave the answer as √63 instead.
The square roots of negative numbers are what we now call imaginary numbers. The first person to suggest that they shouldn’t be ignored was the 16th-century Italian astrologer Jerome Cardano, who was embarked on a grand project: a book detailing all of the algebraic knowledge of his times. While working out cubic equations, he stopped and stared at the issue. At first, he called them “impossible cases.” In his 1545 book on algebra, The Great Art, he gave the example of trying to divide 10 into two numbers that multiply together to make 40. In the process of finding those numbers, you come across 5 + √–15.
Cardano didn’t shy away from this unexpected encounter. In fact, he even jotted down a few thoughts about it. However, he wrote in Latin, and translators argue about what he actually meant. For some, he calls it a “false position.” For others, it’s a “fictitious” number. Still others say he characterizes the situation as “impossible” to solve. One of his further comments on how to proceed in such a situation is translated as “putting aside the mental tortures” and as “the imaginary parts being lost.” Elsewhere he refers to this as “arithmetic subtlety, the end of which … is as refined as it is useless.” He says it “truly is sophisticated … one cannot carry out the other operations one can in the case of a pure negative.” By pure negative, he means a standard negative number, something like –4. He was happy with negative numbers and wrote that “√9 is either +3 or –3, for a plus [times a plus] or a minus times a minus yields a plus.” And then he continued, “√–9 is neither +3 or –3 but is some recondite third sort of thing.” Cardano clearly thought the square roots of negative numbers were something abstruse and abstract, but at the same time he knew they were something—and something that a mathematician should engage with. The task wasn’t for him, though; none of Cardano’s subsequent writings mention the square roots of negative numbers. He left it to his fellow countryman, Rafael Bombelli, to address them a couple of decades or so later.
In what he called a “wild thought,” Bombelli suggested in 1572 that the two terms in 5 + √–15 could be treated as two separate things. “The whole matter seemed to rest on sophistry rather than truth,” he said, but he did it anyway. And we still do it today because it works.
A full mathematical description of nature requires imaginary numbers to exist.
Bombelli’s two separate things were what we now call real numbers and imaginary numbers. The combination of the two is known as a “complex number” (it’s complex as in “military-industrial complex,” speaking of combination—of real and imaginary parts—rather than complication). But let’s be clear. If there’s one thing we’ve learned in our time revisiting mathematics, it’s that all numbers are imaginary. They are simply a notation that helps with the concept of “how many.” So applying the name “imaginary numbers” to the square roots of negative numbers is pejorative and unhelpful.
That said, we should acknowledge a distinction. What mathematicians call “real” numbers are the numbers you’re more familiar with. The “two” in two apples; the 3.14… in pi; the fraction. And just as positive numbers are in a sense complemented by negative numbers, what we call real numbers are complemented by what we now have to call imaginary numbers. Think of them as yin and yang, or heads and tails. And certainly not as actually imaginary.
Bombelli, in his wild thought, demonstrated that this new tribe of numbers have a role to play in the real world. He set out to solve a cubic equation that Cardano had given up on: x3 = 15x + 4. Cardano’s solution required him to deal with an expression that contained the square root of –121, and he just didn’t know where to go with it. Bombelli, on the other hand, thought he might try applying normal rules of arithmetic to the square root. So, he said, maybe √–121 is the same as √121 × √–1, which gives 11 × √–1.
Bombelli’s great breakthrough was to see that these strange, seemingly impossible numbers obey simple arithmetic rules once they are separated out from the other, more familiar types of number during a calculation. Everything after that was just grasping the nettle.
Proceeding with Cardano’s cubic equation, he eventually arrived at a solution:
x = (2 + √–1) + (2 – √–1)
Separate them out into what we would now call their real and imaginary parts, and it simplifies to 2 plus 2, and √–1 minus √–1. The imaginary part disappears, leaving us with just 2 + 2. So x = 4 is one of the solutions to x3 = 15x + 4. Plug it in and check for yourself.
These days, the convention is to use i to represent √–1. The Swiss mathematician Leonard Euler first came up with this. It’s easy to assume that i stands for imaginary, but the truth is, as with his e, Euler may just have picked it at random. Whatever the reason, Euler’s move has cemented i as the imaginary number in a very unhelpful way.
To see better what an imaginary number is, let’s think of a standard number line that runs from –1 to 1 (you can think of it as a ruler placed on a table in front of you, running from –1 on the left to +1 on the right). We call the process of moving along the line addition and subtraction (I’m at 0.3, and I’ll add 0.3 more, which takes me to 0.6). But we can also imagine making some moves by multiplication. If I start at 1, how do I get to –1? I multiply by –1. So let’s picture multiplication by –1 as half a rotation, anticlockwise, around a circle (in our case, the circle passes through 1 and –1). It’s actually a rotation by 180 degrees. In mathematicians’ preferred units to denote angles, 180 degrees is π radians (360°, a whole circle, is 2π radians).
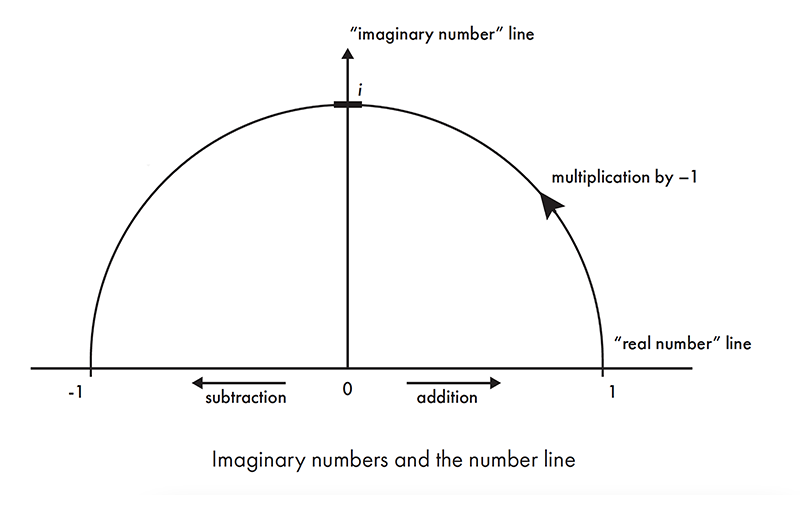
What happens if we only do half of this rotation? It’s halfway to multiplying by –1, which you can think of as the same as multiplying by √–1. That rotation, by just π/2 radians (or 90°) leaves our number up on the top part of the circle’s circumference, away from the standard number line. So we can think of the square root of –1 as sitting on a number line that runs at right angles to the number line we’re familiar with. It’s just another set of numbers, this time on a ruler that meets your other ruler at 90° to form a cross, with +1 at the end furthest from you, and –1 right in front of you.
That leads us somewhere interesting. The link with rotation in circles means that i is related to π and the sines and cosines of angles. That relationship is mediated through the strange number e, often called Euler’s number. This “irrational” number begins with the sequence 2.71828… and goes on forever. It is ubiquitous in mathematics and is vital to statistics, calculus, natural logarithms, and a range of arithmetic calculations. Euler worked out exactly what this looks like by taking a particular kind of infinite series (it’s called a Taylor series), and deriving something now known as Euler’s formula:
e±iθ = cosθ ± isinθ
This shows there is a fundamental relationship between the base of the natural logarithm and the imaginary number. What’s more, you can reduce this to the relation known as the Euler identity:
eiπ + 1 = 0
To some, this is a near-mystical formula. Here we have the base of natural logarithms e; the numbers 0 and 1, which are both unique cases on the whole number line; the imaginary number, a special case all of its own; and π, which as we know is a source of power in mathematics. Despite being discovered at different times by different people looking at different pieces of mathematics, it turns out they are interrelated, coexisting in this elegant, simple equation.
Seen from a slightly different perspective, perhaps we shouldn’t be surprised. As with π itself, there really isn’t anything mystical about this formula. It results from the fact that numbers change and transform themselves and each other through rotations. That only happens because of what numbers are: representations of the relationships between quantities. We don’t find anything mystical about moving along the familiar “real” number line by adding and subtracting. And there’s nothing different, really, about the transformations that come about through multiplications and divisions. Remember that sines and cosines are just ratios—one number divided by another—that are related to the angles within triangles, and you can represent those angles as fractions or multiples of π in units known as radians. So what we’re discovering here is not some deep mystery about the universe, but a clear and useful set of relationships that are a consequence of defining numbers in various different ways.
In fact, these relationships are more than useful—they could be described as vital. Take their application to science, for example: a full mathematical description of nature seems to require imaginary numbers to exist. The “real” numbers, of which we have learned so much, are not enough. They must be combined with the imaginary numbers to form the “complex” numbers that Bombelli first created. The result, says mathematician Roger Penrose, is a beautiful completeness. “Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable,” he says in his book The Road to Reality. “It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales.” In other words, imaginary numbers had to be discovered because they are an essential part of the description of nature.
Michael Brooks is a United Kingdom-based science writer. His most recent book is The Art of More: How Mathematics Created Civilization.
Excerpted from The Art of More: How Mathematics Created Civilization by Michael Brooks. Copyright © 2022 by Michael Brooks. Excerpted by permission of Pantheon Books, a division of Penguin Random House LLC. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher.
Lead image: agsandrew / Shutterstock
https://nautil.us/imaginary-numbers-are ... dium=email

Imaginary numbers are not imaginary at all. The truth is, they have had far more impact on our lives than anything truly imaginary ever could. Without imaginary numbers, and the vital role they played in putting electricity into homes, factories, and internet server-farms, the modern world would not exist. Students who might complain to their math teacher that there’s no point in anyone learning how to use imaginary numbers would have to put down their phone, turn off their music, and pull the wires out of their broadband router. But perhaps we should start with an explanation of what an imaginary number is.
We know by now how to square a number (multiply it by itself), and we know that negative numbers make a positive number when squared; a minus times a minus is a plus, remember? So (–2) × (–2) = 4. We also know that taking a square root is the inverse of squaring. So the possible square roots of 4 are 2 and –2. The imaginary number arises from asking what the square root of –4 would be.
What we’re discovering here is not some deep mystery about the universe.
Surely the question is meaningless? If you square a number, whether positive or negative, the answer is positive. So you can’t do the inverse operation if you start with a negative number. That’s certainly what Heron of Alexandria seemed to think. Heron was the Egyptian architect whose mathematical tricks, written in Stereometrica, gave us the dome of the Hagia Sophia. In the same volume, he showed how to calculate the volume of a truncated square pyramid; that is, a pyramid with the top chopped off. His solution for one example involved subtracting 288 from 225 and finding the square root of the result. The result, though, is a negative number: –63. So the answer would be found via √–63.
For some reason—whether a sense that there was some mistake, or someone copied something down wrong, or because it was so absurd—the manuscripts we have show that Heron ignored the minus sign and gave the answer as √63 instead.
The square roots of negative numbers are what we now call imaginary numbers. The first person to suggest that they shouldn’t be ignored was the 16th-century Italian astrologer Jerome Cardano, who was embarked on a grand project: a book detailing all of the algebraic knowledge of his times. While working out cubic equations, he stopped and stared at the issue. At first, he called them “impossible cases.” In his 1545 book on algebra, The Great Art, he gave the example of trying to divide 10 into two numbers that multiply together to make 40. In the process of finding those numbers, you come across 5 + √–15.
Cardano didn’t shy away from this unexpected encounter. In fact, he even jotted down a few thoughts about it. However, he wrote in Latin, and translators argue about what he actually meant. For some, he calls it a “false position.” For others, it’s a “fictitious” number. Still others say he characterizes the situation as “impossible” to solve. One of his further comments on how to proceed in such a situation is translated as “putting aside the mental tortures” and as “the imaginary parts being lost.” Elsewhere he refers to this as “arithmetic subtlety, the end of which … is as refined as it is useless.” He says it “truly is sophisticated … one cannot carry out the other operations one can in the case of a pure negative.” By pure negative, he means a standard negative number, something like –4. He was happy with negative numbers and wrote that “√9 is either +3 or –3, for a plus [times a plus] or a minus times a minus yields a plus.” And then he continued, “√–9 is neither +3 or –3 but is some recondite third sort of thing.” Cardano clearly thought the square roots of negative numbers were something abstruse and abstract, but at the same time he knew they were something—and something that a mathematician should engage with. The task wasn’t for him, though; none of Cardano’s subsequent writings mention the square roots of negative numbers. He left it to his fellow countryman, Rafael Bombelli, to address them a couple of decades or so later.
In what he called a “wild thought,” Bombelli suggested in 1572 that the two terms in 5 + √–15 could be treated as two separate things. “The whole matter seemed to rest on sophistry rather than truth,” he said, but he did it anyway. And we still do it today because it works.
A full mathematical description of nature requires imaginary numbers to exist.
Bombelli’s two separate things were what we now call real numbers and imaginary numbers. The combination of the two is known as a “complex number” (it’s complex as in “military-industrial complex,” speaking of combination—of real and imaginary parts—rather than complication). But let’s be clear. If there’s one thing we’ve learned in our time revisiting mathematics, it’s that all numbers are imaginary. They are simply a notation that helps with the concept of “how many.” So applying the name “imaginary numbers” to the square roots of negative numbers is pejorative and unhelpful.
That said, we should acknowledge a distinction. What mathematicians call “real” numbers are the numbers you’re more familiar with. The “two” in two apples; the 3.14… in pi; the fraction. And just as positive numbers are in a sense complemented by negative numbers, what we call real numbers are complemented by what we now have to call imaginary numbers. Think of them as yin and yang, or heads and tails. And certainly not as actually imaginary.
Bombelli, in his wild thought, demonstrated that this new tribe of numbers have a role to play in the real world. He set out to solve a cubic equation that Cardano had given up on: x3 = 15x + 4. Cardano’s solution required him to deal with an expression that contained the square root of –121, and he just didn’t know where to go with it. Bombelli, on the other hand, thought he might try applying normal rules of arithmetic to the square root. So, he said, maybe √–121 is the same as √121 × √–1, which gives 11 × √–1.
Bombelli’s great breakthrough was to see that these strange, seemingly impossible numbers obey simple arithmetic rules once they are separated out from the other, more familiar types of number during a calculation. Everything after that was just grasping the nettle.
Proceeding with Cardano’s cubic equation, he eventually arrived at a solution:
x = (2 + √–1) + (2 – √–1)
Separate them out into what we would now call their real and imaginary parts, and it simplifies to 2 plus 2, and √–1 minus √–1. The imaginary part disappears, leaving us with just 2 + 2. So x = 4 is one of the solutions to x3 = 15x + 4. Plug it in and check for yourself.
These days, the convention is to use i to represent √–1. The Swiss mathematician Leonard Euler first came up with this. It’s easy to assume that i stands for imaginary, but the truth is, as with his e, Euler may just have picked it at random. Whatever the reason, Euler’s move has cemented i as the imaginary number in a very unhelpful way.
To see better what an imaginary number is, let’s think of a standard number line that runs from –1 to 1 (you can think of it as a ruler placed on a table in front of you, running from –1 on the left to +1 on the right). We call the process of moving along the line addition and subtraction (I’m at 0.3, and I’ll add 0.3 more, which takes me to 0.6). But we can also imagine making some moves by multiplication. If I start at 1, how do I get to –1? I multiply by –1. So let’s picture multiplication by –1 as half a rotation, anticlockwise, around a circle (in our case, the circle passes through 1 and –1). It’s actually a rotation by 180 degrees. In mathematicians’ preferred units to denote angles, 180 degrees is π radians (360°, a whole circle, is 2π radians).

What happens if we only do half of this rotation? It’s halfway to multiplying by –1, which you can think of as the same as multiplying by √–1. That rotation, by just π/2 radians (or 90°) leaves our number up on the top part of the circle’s circumference, away from the standard number line. So we can think of the square root of –1 as sitting on a number line that runs at right angles to the number line we’re familiar with. It’s just another set of numbers, this time on a ruler that meets your other ruler at 90° to form a cross, with +1 at the end furthest from you, and –1 right in front of you.
That leads us somewhere interesting. The link with rotation in circles means that i is related to π and the sines and cosines of angles. That relationship is mediated through the strange number e, often called Euler’s number. This “irrational” number begins with the sequence 2.71828… and goes on forever. It is ubiquitous in mathematics and is vital to statistics, calculus, natural logarithms, and a range of arithmetic calculations. Euler worked out exactly what this looks like by taking a particular kind of infinite series (it’s called a Taylor series), and deriving something now known as Euler’s formula:
e±iθ = cosθ ± isinθ
This shows there is a fundamental relationship between the base of the natural logarithm and the imaginary number. What’s more, you can reduce this to the relation known as the Euler identity:
eiπ + 1 = 0
To some, this is a near-mystical formula. Here we have the base of natural logarithms e; the numbers 0 and 1, which are both unique cases on the whole number line; the imaginary number, a special case all of its own; and π, which as we know is a source of power in mathematics. Despite being discovered at different times by different people looking at different pieces of mathematics, it turns out they are interrelated, coexisting in this elegant, simple equation.
Seen from a slightly different perspective, perhaps we shouldn’t be surprised. As with π itself, there really isn’t anything mystical about this formula. It results from the fact that numbers change and transform themselves and each other through rotations. That only happens because of what numbers are: representations of the relationships between quantities. We don’t find anything mystical about moving along the familiar “real” number line by adding and subtracting. And there’s nothing different, really, about the transformations that come about through multiplications and divisions. Remember that sines and cosines are just ratios—one number divided by another—that are related to the angles within triangles, and you can represent those angles as fractions or multiples of π in units known as radians. So what we’re discovering here is not some deep mystery about the universe, but a clear and useful set of relationships that are a consequence of defining numbers in various different ways.
In fact, these relationships are more than useful—they could be described as vital. Take their application to science, for example: a full mathematical description of nature seems to require imaginary numbers to exist. The “real” numbers, of which we have learned so much, are not enough. They must be combined with the imaginary numbers to form the “complex” numbers that Bombelli first created. The result, says mathematician Roger Penrose, is a beautiful completeness. “Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable,” he says in his book The Road to Reality. “It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales.” In other words, imaginary numbers had to be discovered because they are an essential part of the description of nature.
Michael Brooks is a United Kingdom-based science writer. His most recent book is The Art of More: How Mathematics Created Civilization.
Excerpted from The Art of More: How Mathematics Created Civilization by Michael Brooks. Copyright © 2022 by Michael Brooks. Excerpted by permission of Pantheon Books, a division of Penguin Random House LLC. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher.
Lead image: agsandrew / Shutterstock
https://nautil.us/imaginary-numbers-are ... dium=email
12 Mind-Bending Perceptual Illusions
Everyone loves a good optical illusion. Most people first come across them as kids, and are instantly transfixed. And most of us never quite outgrow them. Even cats seem to enjoy the occasional optical illusion!
The good news, then, for humans and nonhumans alike, is that our illusions seem to be getting better over time. In the age of social media, lots of people are making and sharing them, and the best ones are quickly going viral and setting the new standard. In effect, our illusions are evolving culturally to be more and more powerful.
But although perceptual illusions are fun, they also have important philosophical implications. They show us in a clear and unambiguous way that we don’t directly perceive the world around us. Perceptual experience is a simulation—a mental model—that doesn’t always correspond to the reality it aims to depict.
The following illusions are some of my favorites. Enjoy!
1. The Power of Top-Down Processing
To get the ball rolling, here’s a good example of how expectations guide perception.

Breezy Clothing
We’re so used to words being arranged in a certain order that, when the words are jumbled up, we often don’t notice: We mistake our expectations for the world. That’s why proofreading your own essays is so hard.
2. The Skye Blue Café Wall Illusion
This illusion, created by the artist Victoria Skye, was one of the top entries in the 2017 Best Illusion of the Year Contest. Believe it or not, the horizontal lines are all perfectly parallel. To prove this to yourself, just squint at the image or look at it from the side.

Victoria Skye
Notice that, even after you’re completely convinced that the lines are parallel, the illusion continues to work. Perception is largely involuntary—and in many ways is walled off from our abstract knowledge of the world.
3. Confetti
This one’s a variation on the Munker Illusion, created by David Novick. The circles in the image are all the same color. The only thing that differs is the color of the lines around them.

David Novick
The illusion is a vivid demonstration of the fact that we don’t directly perceive the colors of objects in the world. Instead, the perceptual system takes an educated “guess,” based on the objects’ surroundings.
4. The Rice Wave Illusion
This might look an animated GIF, but it’s not. The movement is all in your head.

Akiyoshi Kitaoka
The shading and sequencing of the yellow blobs triggers the motion areas of the brain, creating a perception of movement in a stimulus that’s actually static. Interestingly, around 5 percent of people seem to be immune to this illusion.
5. The Tilted Road Illusion
This looks like two photos of the same road, taken from different angles. But it’s actually just the same photo twice.

Daniel Picon
Apparently, the visual system treats the image as if it were a single photo of two separate roads. The outlines of the two roads are parallel to one another in the two-dimensional image. For that to be the case in the image, the actual roads in the real world would have to be angling strongly away from each other. So, that’s what the visual system infers.
6. Lightness Illusion
This one comes from master illusion-maker Akiyoshi Kitaoka (@AkiyoshiKitaoka).

In trying to make sense of the video, the visual system acts as if the gray square is being moved out of shadow into bright light, and then into dark shadow. For the square to look that shade in bright light, it would have to be quite dark—so the perpetual system infers that it is. Conversely, for the square to look that shade in dark shadow, it would have to be very light—so the perceptual system infers that, instead.
Your brain is doing a lot of work behind the scenes—more than you might have imagined!
7. The Dynamic Ebbinghaus
Another award-winning illusion. The orange circle doesn’t actually change size.

As with color and lightness, we don’t directly perceive the size of objects. The perceptual system makes an inference about their size, based on clues in our sense data—including the relative size of other, nearby objects.
8. The Dynamic Müller-Lyer Illusion
This is one of the best illusions I’ve seen. The blue and red lines are all the same length; none is moving or changing size, and they’re all at the same level. Only the arrowheads are moving.
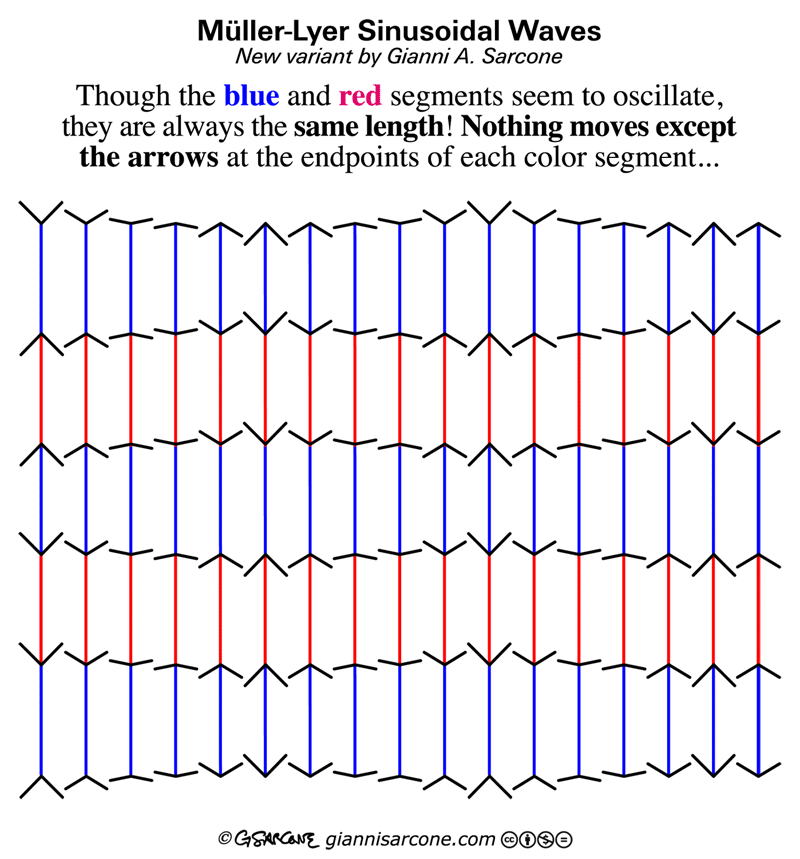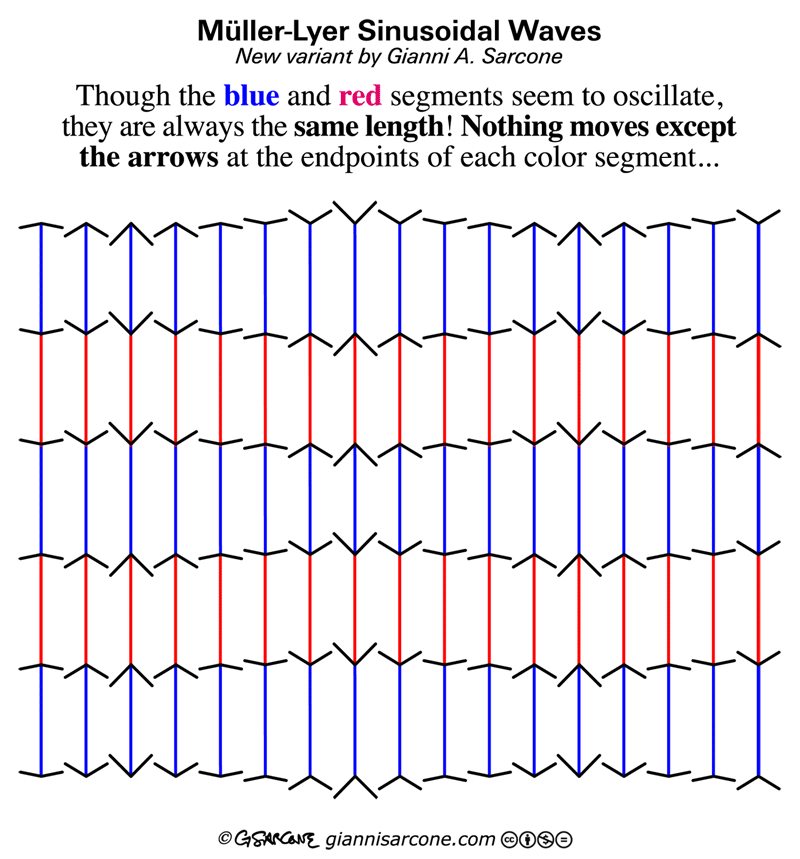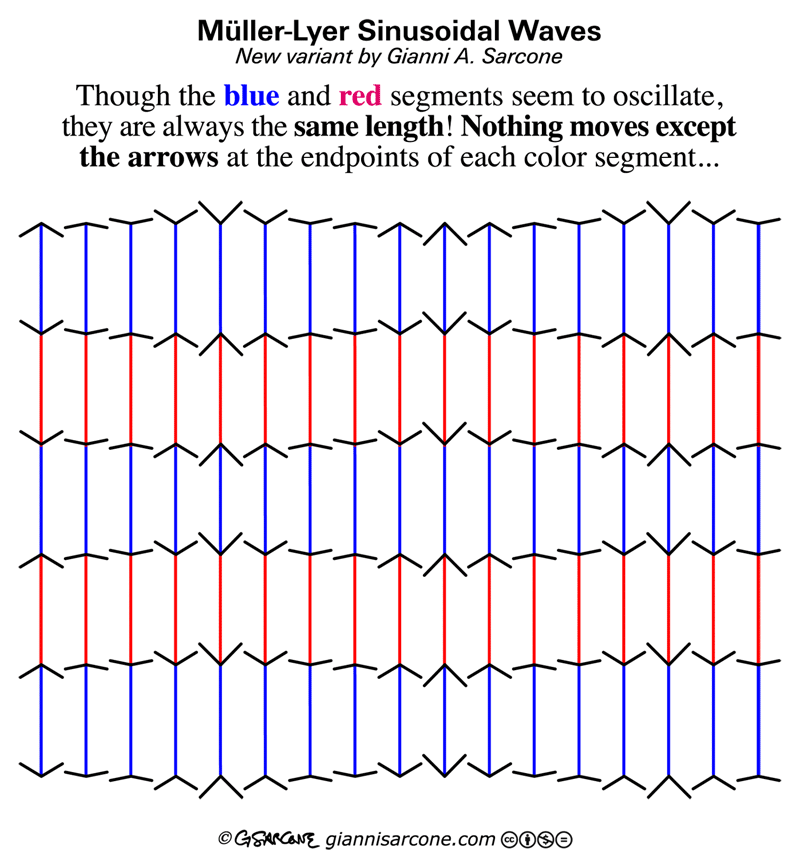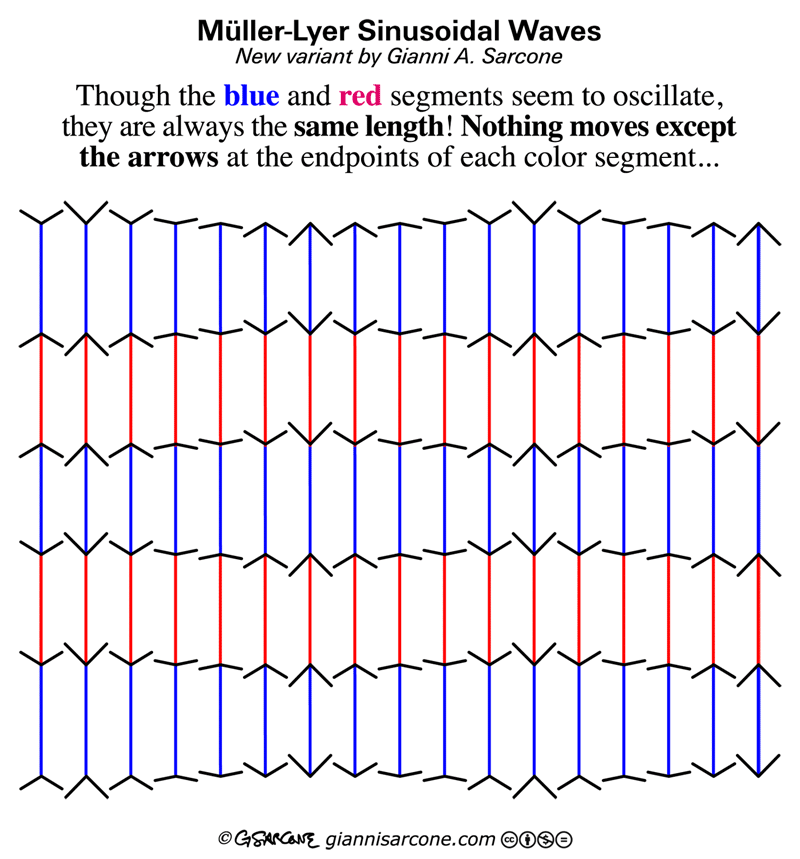
The illusion is a new variation on an old theme: the Müller-Lyer illusion. There are many theories about how this works, but no one’s 100 percent sure. There’s even debate about whether it works for all human beings everywhere, or instead is a culture-specific phenomenon.
9. The Train Illusion
You can make the train change direction with the power of your mind … and you can get better at it with practice.

Perception always involves going beyond the evidence of the senses. In this case, the evidence is relatively sparse, such that there are two plausible interpretations: The train is coming or the train is going. We can choose to see it either way.
10. Rotating Rings
This one freaks a lot of people out. Every time you switch from looking at the red dot to the yellow, or vice versa, both wheels start spinning in the opposite direction. The illusion exploits differences in the way we interpret motion in the center of the visual field vs. the periphery.
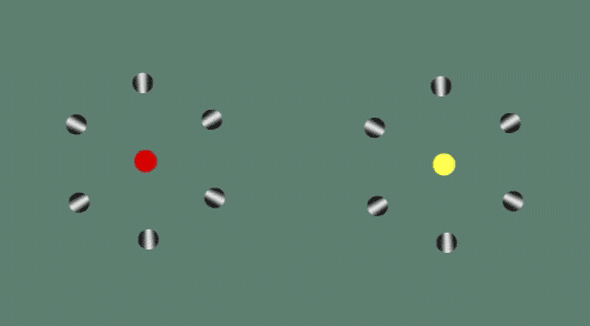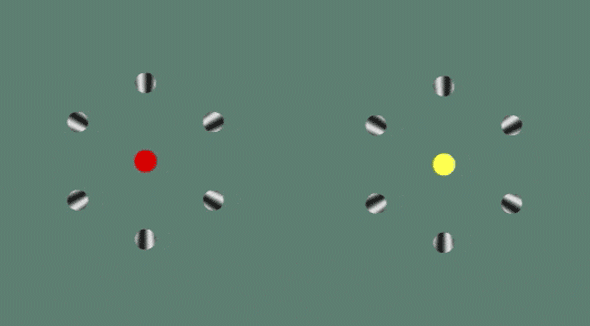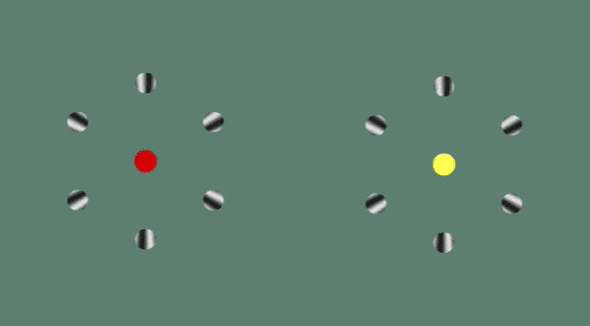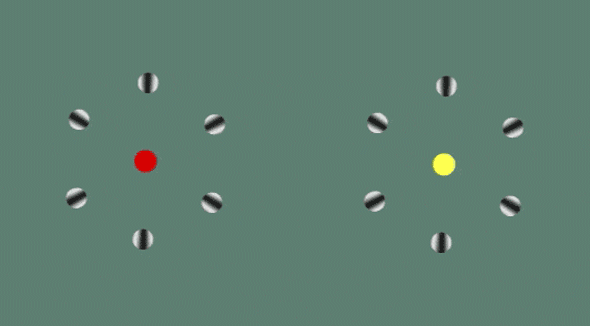
11. The Spinning Dancer
One of my all-time favorites. If you look at the dancer on the left and the one in the middle, the one in the middle spins clockwise. If you instead look at the dancer on the right and the one in the middle, the one in the middle starts spinning counter-clockwise.

As with the train illusion, the secret is that the center image is ambiguous: It can be interpreted as a dancer spinning in either direction. The dancers on the left and right, in contrast, include additional details which force one or other interpretation. This forced interpretation then guides our perception of the middle, ambiguous figure.
12. The Starry Night
Stare at the center of the top image for 30 seconds then check out Van Gogh’s Starry Night …

This is an example of a motion aftereffect. As you stare at the spiral, your visual system begins compensating for the motion so it can ignore this predictable stimulus. But then, when you look at the stationary painting, the system keeps compensating for the motion: motion that’s no longer there. This creates a false perception of motion in the opposite direction, which interacts with the details of the painting.
Steve Stewart-Williams is author of The Ape That Understood the Universe: How the Mind and Culture Evolve (Cambridge University Press, 2018).
The good news, then, for humans and nonhumans alike, is that our illusions seem to be getting better over time. In the age of social media, lots of people are making and sharing them, and the best ones are quickly going viral and setting the new standard. In effect, our illusions are evolving culturally to be more and more powerful.
But although perceptual illusions are fun, they also have important philosophical implications. They show us in a clear and unambiguous way that we don’t directly perceive the world around us. Perceptual experience is a simulation—a mental model—that doesn’t always correspond to the reality it aims to depict.
The following illusions are some of my favorites. Enjoy!
1. The Power of Top-Down Processing
To get the ball rolling, here’s a good example of how expectations guide perception.

Breezy Clothing
We’re so used to words being arranged in a certain order that, when the words are jumbled up, we often don’t notice: We mistake our expectations for the world. That’s why proofreading your own essays is so hard.
2. The Skye Blue Café Wall Illusion
This illusion, created by the artist Victoria Skye, was one of the top entries in the 2017 Best Illusion of the Year Contest. Believe it or not, the horizontal lines are all perfectly parallel. To prove this to yourself, just squint at the image or look at it from the side.

Victoria Skye
Notice that, even after you’re completely convinced that the lines are parallel, the illusion continues to work. Perception is largely involuntary—and in many ways is walled off from our abstract knowledge of the world.
3. Confetti
This one’s a variation on the Munker Illusion, created by David Novick. The circles in the image are all the same color. The only thing that differs is the color of the lines around them.

David Novick
The illusion is a vivid demonstration of the fact that we don’t directly perceive the colors of objects in the world. Instead, the perceptual system takes an educated “guess,” based on the objects’ surroundings.
4. The Rice Wave Illusion
This might look an animated GIF, but it’s not. The movement is all in your head.

Akiyoshi Kitaoka
The shading and sequencing of the yellow blobs triggers the motion areas of the brain, creating a perception of movement in a stimulus that’s actually static. Interestingly, around 5 percent of people seem to be immune to this illusion.
5. The Tilted Road Illusion
This looks like two photos of the same road, taken from different angles. But it’s actually just the same photo twice.

Daniel Picon
Apparently, the visual system treats the image as if it were a single photo of two separate roads. The outlines of the two roads are parallel to one another in the two-dimensional image. For that to be the case in the image, the actual roads in the real world would have to be angling strongly away from each other. So, that’s what the visual system infers.
6. Lightness Illusion
This one comes from master illusion-maker Akiyoshi Kitaoka (@AkiyoshiKitaoka).

In trying to make sense of the video, the visual system acts as if the gray square is being moved out of shadow into bright light, and then into dark shadow. For the square to look that shade in bright light, it would have to be quite dark—so the perpetual system infers that it is. Conversely, for the square to look that shade in dark shadow, it would have to be very light—so the perceptual system infers that, instead.
Your brain is doing a lot of work behind the scenes—more than you might have imagined!
7. The Dynamic Ebbinghaus
Another award-winning illusion. The orange circle doesn’t actually change size.

As with color and lightness, we don’t directly perceive the size of objects. The perceptual system makes an inference about their size, based on clues in our sense data—including the relative size of other, nearby objects.
8. The Dynamic Müller-Lyer Illusion
This is one of the best illusions I’ve seen. The blue and red lines are all the same length; none is moving or changing size, and they’re all at the same level. Only the arrowheads are moving.

The illusion is a new variation on an old theme: the Müller-Lyer illusion. There are many theories about how this works, but no one’s 100 percent sure. There’s even debate about whether it works for all human beings everywhere, or instead is a culture-specific phenomenon.
9. The Train Illusion
You can make the train change direction with the power of your mind … and you can get better at it with practice.

Perception always involves going beyond the evidence of the senses. In this case, the evidence is relatively sparse, such that there are two plausible interpretations: The train is coming or the train is going. We can choose to see it either way.
10. Rotating Rings
This one freaks a lot of people out. Every time you switch from looking at the red dot to the yellow, or vice versa, both wheels start spinning in the opposite direction. The illusion exploits differences in the way we interpret motion in the center of the visual field vs. the periphery.

11. The Spinning Dancer
One of my all-time favorites. If you look at the dancer on the left and the one in the middle, the one in the middle spins clockwise. If you instead look at the dancer on the right and the one in the middle, the one in the middle starts spinning counter-clockwise.

As with the train illusion, the secret is that the center image is ambiguous: It can be interpreted as a dancer spinning in either direction. The dancers on the left and right, in contrast, include additional details which force one or other interpretation. This forced interpretation then guides our perception of the middle, ambiguous figure.
12. The Starry Night
Stare at the center of the top image for 30 seconds then check out Van Gogh’s Starry Night …

This is an example of a motion aftereffect. As you stare at the spiral, your visual system begins compensating for the motion so it can ignore this predictable stimulus. But then, when you look at the stationary painting, the system keeps compensating for the motion: motion that’s no longer there. This creates a false perception of motion in the opposite direction, which interacts with the details of the painting.
Steve Stewart-Williams is author of The Ape That Understood the Universe: How the Mind and Culture Evolve (Cambridge University Press, 2018).
Math Is the Great Secret

By Alec Wilkinson
Mr. Wilkinson is the author of “A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age.”
As a boy in the first weeks of algebra class, I felt confused and then I went sort of numb. Adolescents order the world from fragments of information. In its way, adolescence is a kind of algebra. The unknowns can be determined but doing so requires a special aptitude, not to mention a comfort with having things withheld. Straightforward, logical thinking is required, and a willingness to follow rules, which aren’t evenly distributed adolescent capabilities.
When I thought about mathematics at all as a boy it was to speculate about why I was being made to learn it, since it seemed plainly obvious that there was no need for it in adult life. Balancing a checkbook or drawing up a budget was the answer we were given for how math would prove necessary later, but you don’t need algebra or geometry or calculus to do either of those things.
But if I had understood how deeply mathematics is embedded in the world, how it figures in every gesture we make, whether crossing a crowded street or catching a ball, how it figures in painting and perspective and in architecture and in the natural world and so on, then perhaps I might have seen it the way the ancients had seen it, as a fundamental part of the world’s design, perhaps even the design itself. If I had felt that the world was connected in its parts, I might have been provoked to a kind of wonder and enthusiasm. I might have wanted to learn.
Five years ago, when I was 65, I decided to see if I could learn adolescent mathematics — algebra, geometry and calculus — because I had done poorly at algebra and geometry and I hadn’t taken calculus at all. I didn’t do well at it the second time, either, but I have become a kind of math evangelist.
Mathematics, I now see, is important because it expands the world. It is a point of entry into larger concerns. It teaches reverence. It insists one be receptive to wonder. It requires that a person pay close attention. To be made to consider a problem carefully discourages scattershot and slovenly thinking and encourages systematic thought, an advantage, so far as I can tell, in all endeavors. Abraham Lincoln said he spent a year reading Euclid in order to learn to think logically.
Studying adolescent mathematics, a person is crossing territory on which footprints have been left since antiquity. Some of the trails have been made by distinguished figures, but the bulk of them have been left by ordinary people like me. As a boy, trying to follow a path in a failing light, I never saw the mysteries I was moving among, but on my second pass I began to. Nothing had changed about math, but I had changed. The person I had become was someone whom I couldn’t have imagined as an adolescent. Math was different, because I was different.
The beginner math mystery, available to anyone, concerns the origin of numbers. It’s a simple speculation: Where do numbers come from? No one knows. Were they invented by human beings? Hard to say. They appear to be embedded in the world in ways that we can’t completely comprehend. They began as measurements of quantities and grew into the means for the most precise expressions of the physical world — e = mc², for example.
The second mystery is that of prime numbers, those numbers such as 2, 3, 5, 7, 11 and 13 that can be divided cleanly only by one or by themselves. All numbers not prime are called composite numbers, and all composite numbers are the result of a unique arrangement of primes: 2 x 2 = 4. 2 x 3= 6. 2 x 2 x 2 = 8. 3 x 3= 9. 2 x 3 x 3 x 37 = 666. 29 x 31 = 899. 2 x 2 x 2 x 5 x 5 x 5 = 1,000. If human beings invented numbers and counting, then how is it that there are numbers such as primes that have attributes no one gave them? The grand and enfolding mystery is whether mathematics is created by human beings or exists independently of us in a territory adjacent to the actual world, the location of which no one can specify. Plato called it the non-spatiotemporal realm. It is the timeless nowhere that never has and never will exist anywhere but that nevertheless is.
Mathematics is one of the most efficient means of approaching the great secret, of considering what lies past all that we can see or presently imagine. Mathematics doesn’t describe the secret so much as it implies that there is one.
On my second engagement, whenever I encountered a definition of mathematics, I wrote it down. Among those I liked best was that mathematics is a story that has been being written for thousands of years, is always being added to and might never be finished. Such a thought would have appealed to me deeply as a boy and might have made mathematics seem maybe not welcoming, but at least less forbidding than it appeared.
https://www.nytimes.com/2022/09/18/opin ... 778d3e6de3
Re: Concept of Knowledge Revisited
I Teach the Humanities, and I Still Don’t Know What Their Value Is
If a group of math students fails to learn the material, that might be because the teacher is not trying hard enough or because she has been inappropriately tasked with, for example, teaching calculus to toddlers. Supposing, however, that neither of these things is true — the teacher is passionately invested in teaching, and she has many suitable students — yet her students all fail the final exam, eventually we would be forced to say that she might not know math so well.
I believe that we humanists are in the position of this math teacher. We have been issuing a steady stream of defenses of the humanities for many decades now, but the crisis of the humanities only grows. In the face of declining student interest and mounting political scrutiny, universities and colleges are increasingly putting humanities departments on the chopping block.
We humanists keep on trying to teach people what the value of the humanities is, and people keep failing to learn our lessons. This suggests to me that humanists do not know the value of the thing they are trying to defend. We can spout pieties that sound inspiring to those already convinced of our cause, but so too can an ignorant math teacher “teach” math to those who already know it.
As a humanist — someone who reads, teaches and researches primarily philosophy but also, on the side, novels and poems and plays and movies — I am prepared to come out and admit that I do not know what the value of the humanities is. I do not know whether the study of the humanities promotes democracy or improves your moral character or enriches your leisure time or improves your critical thinking skills or increases your empathy.
You might be surprised to learn that this bit of ignorance poses no obstacle to me in the classroom. I suppose it would if I approached the teaching of Descartes as a matter of explaining why reading Descartes will make you a better person, but that is not how I teach Descartes, nor does any philosopher I know teach Descartes in that way. I am there to lay out the premises of his reasoning, to explain some of the relevant concepts, to entertain questions and objections and to work through the arguments together with the students to see if they hold water. We are searching, trying to find the value that may be there.
I once asked the best teacher I ever had why she no longer taught her favorite novel, and she said that she stopped teaching a book when she found she was no longer curious about it. The humanistic spirit is, fundamentally, an inquisitive one.
In contrast, defenses of the humanities are not — and cannot be — conducted in an inquisitive spirit, because a defensive spirit is inimical to an inquisitive one. Defensiveness is, it must be admitted, an understandable response when budgets are being cut and the chopping block is brought out and you need to explain why you shouldn’t be on it. It may be that humanists need to spend some of our time joining political battles, which, like all political battles, require their participants to pretend to know things that they do not actually know.
Nonetheless, we should be alert to the danger of becoming accustomed to putting our worst foot forward. An atmosphere of urgency and calls for immediate action are hostile to fields of study like literature and philosophy that require a contemplative mood, and the pretense of knowing what one doesn’t actually know is hostile to forms of inquiry that demand an open mind.
A defensive mind-set also encourages politicization. If the study of literature or philosophy helps to fight sexism and racism or to promote democracy and free speech — and everyone agrees that sexism and racism are bad and democracy and free speech are good — then you have your answer as to why we shouldn’t cut funding for the study of literature or philosophy. Politicization is a way of arming the humanities for its political battles, but it comes at an intellectual cost. Why are sexism and racism so bad? Why is democracy so good? Politicization silences these and other questions, whereas the function of the humanities is to raise them.
Defensiveness also threatens to infect our work as humanists. A posture that we initially assumed for the purposes of confronting skeptics comes to restructure how we talk to our students, how we construct our syllabuses and even how we read the texts we assign, which now must prove themselves useful toward whichever political goals currently receive the stamp of approval.
Humanists are not alone in their ignorance about the purpose of their disciplines. Mathematicians or economists or biologists might mutter something about practical applications of their work, but very few serious scholars confine their research to some narrow pragmatic agenda. The difference between the humanists and the scientists is simply that scientists are under a lot less pressure to explain why they exist, because the society at large believes itself to already have the answer to that question. If physics were constantly out to justify itself, it would become politicized, too, and physicists would also start spouting pious platitudes about how physics enriches your life.
I will admit that every time I hear of a classics department being cut, it hurts. I may not know why it is important to read Homer and Plato, but I do have a deep love for reading, teaching and pondering those texts. That love is what I have to share with others, as well as the surprise and delight of finding that people thousands of years dead can be one’s partners in inquiry.
If at some point I am called on to defend the study of Homer or Descartes at some official hearing, I will do my best, but I do not deem it right to change my approach to what I study and teach in anticipation of that encounter. I will not run to battle; the battle will have to come to me.
The task of humanists is to invite, to welcome, to entice, to excite, to engage. And when we let ourselves be ourselves, when we allow the humanistic spirit that animates us to flow out not only into our classrooms but also in our public-self presentation, we find we don’t need to defend or prove anything: We are irresistible.
Are the humanities valuable? What is their value? These are good questions, they are worth asking, and if humanists don’t ask them, no one will. But remember: No one can genuinely ask a question to which she thinks she already has the answer.
https://www.nytimes.com/2023/12/02/opin ... 778d3e6de3
If a group of math students fails to learn the material, that might be because the teacher is not trying hard enough or because she has been inappropriately tasked with, for example, teaching calculus to toddlers. Supposing, however, that neither of these things is true — the teacher is passionately invested in teaching, and she has many suitable students — yet her students all fail the final exam, eventually we would be forced to say that she might not know math so well.
I believe that we humanists are in the position of this math teacher. We have been issuing a steady stream of defenses of the humanities for many decades now, but the crisis of the humanities only grows. In the face of declining student interest and mounting political scrutiny, universities and colleges are increasingly putting humanities departments on the chopping block.
We humanists keep on trying to teach people what the value of the humanities is, and people keep failing to learn our lessons. This suggests to me that humanists do not know the value of the thing they are trying to defend. We can spout pieties that sound inspiring to those already convinced of our cause, but so too can an ignorant math teacher “teach” math to those who already know it.
As a humanist — someone who reads, teaches and researches primarily philosophy but also, on the side, novels and poems and plays and movies — I am prepared to come out and admit that I do not know what the value of the humanities is. I do not know whether the study of the humanities promotes democracy or improves your moral character or enriches your leisure time or improves your critical thinking skills or increases your empathy.
You might be surprised to learn that this bit of ignorance poses no obstacle to me in the classroom. I suppose it would if I approached the teaching of Descartes as a matter of explaining why reading Descartes will make you a better person, but that is not how I teach Descartes, nor does any philosopher I know teach Descartes in that way. I am there to lay out the premises of his reasoning, to explain some of the relevant concepts, to entertain questions and objections and to work through the arguments together with the students to see if they hold water. We are searching, trying to find the value that may be there.
I once asked the best teacher I ever had why she no longer taught her favorite novel, and she said that she stopped teaching a book when she found she was no longer curious about it. The humanistic spirit is, fundamentally, an inquisitive one.
In contrast, defenses of the humanities are not — and cannot be — conducted in an inquisitive spirit, because a defensive spirit is inimical to an inquisitive one. Defensiveness is, it must be admitted, an understandable response when budgets are being cut and the chopping block is brought out and you need to explain why you shouldn’t be on it. It may be that humanists need to spend some of our time joining political battles, which, like all political battles, require their participants to pretend to know things that they do not actually know.
Nonetheless, we should be alert to the danger of becoming accustomed to putting our worst foot forward. An atmosphere of urgency and calls for immediate action are hostile to fields of study like literature and philosophy that require a contemplative mood, and the pretense of knowing what one doesn’t actually know is hostile to forms of inquiry that demand an open mind.
A defensive mind-set also encourages politicization. If the study of literature or philosophy helps to fight sexism and racism or to promote democracy and free speech — and everyone agrees that sexism and racism are bad and democracy and free speech are good — then you have your answer as to why we shouldn’t cut funding for the study of literature or philosophy. Politicization is a way of arming the humanities for its political battles, but it comes at an intellectual cost. Why are sexism and racism so bad? Why is democracy so good? Politicization silences these and other questions, whereas the function of the humanities is to raise them.
Defensiveness also threatens to infect our work as humanists. A posture that we initially assumed for the purposes of confronting skeptics comes to restructure how we talk to our students, how we construct our syllabuses and even how we read the texts we assign, which now must prove themselves useful toward whichever political goals currently receive the stamp of approval.
Humanists are not alone in their ignorance about the purpose of their disciplines. Mathematicians or economists or biologists might mutter something about practical applications of their work, but very few serious scholars confine their research to some narrow pragmatic agenda. The difference between the humanists and the scientists is simply that scientists are under a lot less pressure to explain why they exist, because the society at large believes itself to already have the answer to that question. If physics were constantly out to justify itself, it would become politicized, too, and physicists would also start spouting pious platitudes about how physics enriches your life.
I will admit that every time I hear of a classics department being cut, it hurts. I may not know why it is important to read Homer and Plato, but I do have a deep love for reading, teaching and pondering those texts. That love is what I have to share with others, as well as the surprise and delight of finding that people thousands of years dead can be one’s partners in inquiry.
If at some point I am called on to defend the study of Homer or Descartes at some official hearing, I will do my best, but I do not deem it right to change my approach to what I study and teach in anticipation of that encounter. I will not run to battle; the battle will have to come to me.
The task of humanists is to invite, to welcome, to entice, to excite, to engage. And when we let ourselves be ourselves, when we allow the humanistic spirit that animates us to flow out not only into our classrooms but also in our public-self presentation, we find we don’t need to defend or prove anything: We are irresistible.
Are the humanities valuable? What is their value? These are good questions, they are worth asking, and if humanists don’t ask them, no one will. But remember: No one can genuinely ask a question to which she thinks she already has the answer.
https://www.nytimes.com/2023/12/02/opin ... 778d3e6de3
Re: Concept of Knowledge Revisited
The Next Battle in Higher Ed May Strike at Its Soul: Scholarship
Cases involving Stanford, Harvard and M.I.T. are fueling skepticism over the thoroughness of research — even from the academic world’s biggest stars

The next big battle over higher education promises to look at plagiarism.Credit...Sophie Park for The New York Times
Marc Tessier-Lavigne, president of Stanford, resigned in August after an investigation found serious flaws in studies he had supervised going back decades.
Claudine Gay, president of Harvard, resigned as the new year dawned, under mounting accusations of plagiarism going back to her graduate student days.
Then Neri Oxman, a former star professor at M.I.T., was accused of plagiarizing from Wikipedia, among other sources, in her dissertation. Her husband, the hedge-fund billionaire Bill Ackman, was one of Dr. Gay’s most dogged critics. And he has vowed to scour the records of M.I.T.’s faculty, and its president, Sally Kornbluth, for plagiarism.
The attacks on the integrity of higher education have come fast and furious over the last few years. The federal Varsity Blues investigation, in which wealthy parents were accused of using bribery and fraud to secure spots for their children in résumé-building colleges, launched a debate over merit and the admissions game. The affirmative action lawsuit against Harvard exposed how Asian American students must perform at a higher standard to win entry. And the protests over the Israel-Hamas war opened administrators to charges that they tolerated antisemitism on their campuses.
Now the focus has moved into what may be the very soul of higher education: scholarship.
Image
Marc Tessier-Lavigne, in a blue suit, stands outside on the Stanford campus.

Marc Tessier-Lavigne, the former president of Stanford University.Credit...Carolyn Fong for The New York Times
There are differences among the cases — Dr. Tessier-Lavigne and Dr. Gay were the faces of their institutions, while Dr. Oxman is a former faculty member, who was well known in her field of computational design. Defenders of Dr. Gay and Dr. Oxman say that their lifting of words is minor, and that they were not accused of stealing ideas. And unlike Dr. Tessier-Lavigne, they have not had to retract any papers.
But the recent controversies have helped fuel the skepticism that some scholarship is not as rigorous as it purports to be.
“It does strike me that this is a problem of the universities’ own making,” said Ivan Oransky, co-founder of Retraction Watch, which keeps a database of retracted papers now numbering more than 46,000.
“They have tried every which way to avoid acknowledging just how common misconduct is in academia, and what that does is give ammunition to sometimes — let’s face it — bad-faith actors who want to undermine confidence or undermine the reputation of an institution,” Dr. Oransky said.
There is probably more to come. A congressional committee has announced that it would investigate a “hostile takeover” of higher education by “political activists, woke faculty and partisan administrators.”
A cottage industry of checking research papers had already sprung up in the last two decades, including Retraction Watch, the Center for Open Science and Data Colada, a blog dedicated to unmasking research based on bad data.
The number of retracted research papers has grown dramatically over time, to more than 10,000 retractions internationally in 2023, an annual record, according to the journal Nature, up from about 400 papers in 2010, when Retraction Watch began its work, Dr. Oransky said.
This may be in part because the scrutiny has intensified, he said. Nature also blamed the rise of paper-writing mills.
“What’s different this time is the levels at which this seems to be striking — Harvard and Stanford,” Dr. Oransky said. “These are cataclysmic events.”
Dr. Gay, a professor of government and African and African American studies, asked for a handful of corrections in citation and quotation in her dissertation and scholarly papers. But she stood by her work, and an outside panel cleared her of research misconduct.
A review panel found that Dr. Tessier-Lavigne, a neuroscientist, had not personally engaged in or known about data manipulation but that “there may have been opportunities to improve laboratory oversight and management.” He agreed to retract three papers and correct two more.
Dr. Oxman, a celebrated architect and designer, apologized on social media for some lapses in attribution in her dissertation.
Not everyone thinks academia is rife with deception.
Stephen Voss, an associate professor of political science at the University of Kentucky, said he was dismayed that in their attempts to defend Dr. Gay, some academics had suggested that plagiarism was commonplace within their ranks.
“I viewed some of these defenses of Claudine as being false confessions to misbehavior that actually is not taking place at the level her defenders wanted to suggest,” Dr. Voss said. “The ‘it goes on all the time’ argument.”
Dr. Gay is accused of copying, with only light paraphrasing, two passages from Dr. Voss’s work in her dissertation.
Dr. Voss said he was not troubled by it, since he had been her teaching fellow at Harvard, helping to teach her quantitative analysis, and later her colleague in the same lab. “It would have been quite natural for her to borrow ideas from me,” he said. “The Claudine Gay story is just going to force everybody to be a little more careful about citations.”
The internet and software like Turnitin, which targets academic publishing and research, may make it easier to detect plagiarism. And plagiarism watchers are waiting to see what the future of artificial intelligence will bring — more plagiarism or better detection?
But until now, that software has been used more against students than against professors and administrators.
Many scholars are worried that attacks on research will be used by politicians, donors and even other scholars as a pretext to go after their ideological enemies.
“A broad suspicion toward intellectuals and academics is a rich vein in American culture, and recent events have supported it,” Dr. Voss said.
Mr. Ackman, head of the hedge fund Pershing Square Capital Management, was a vocal critic of Dr. Gay’s leadership at Harvard, from her handling of antisemitism on campus to her support for diversity, equity and inclusion policies. The accusations of plagiarism against her became part of his attack.
After Dr. Gay announced that she would resign from her presidency but remain on the faculty, Mr. Ackman posted on X: “There would be nothing wrong with her staying on the faculty if she didn’t have serious plagiarism issues. Students are forced to withdraw for much less.”
Mr. Ackman declined to comment for this article.
It’s this kind of attack that concerns Jonathan Bailey, a copyright and plagiarism consultant who also runs the website Plagiarism Today. “There’s a lot of worry that the heat has been turned up and the people who are doing the evaluations don’t necessarily have academic research or journalistic integrity in mind,” he said.
Just as new accusations dribbled out against Dr. Gay until the day before she resigned, they have continued against Dr. Oxman. On Thursday, Retraction Watch posted a blog item saying that her thesis lifted about 100 words without quotation or citation from an article published in Physics World in 2000. The blog said it learned of the overlap from Steve Haake, a sports engineer who wrote the original article.
“I have never intentionally presented someone else’s words or ideas as my own,” Dr. Oxman said in a statement emailed through a spokesman for her husband on Friday, the day after the Retraction Watch item appeared. “In the process of writing a 330-page dissertation, I missed a couple of footnotes and some quotation marks. Had A.I. software been available in 2009, I could have avoided these errors. The mistakes are simply a function of my humanity.”
Even so, the attacks on academic integrity are sure to continue. “While President Gay’s resignation is welcome news, the problems at Harvard are much larger than one leader, and the committee’s oversight will continue,” said Representative Virginia Foxx, a North Carolina Republican, who heads the House Education and the Workforce Committee, after Dr. Gay’s resignation on Jan. 2.
Image
Rep. Virginia Foxx, a North Carolina Republican, sits at a table.

Representative Virginia Foxx promises to continue her investigation into higher education. Credit...Elizabeth D. Herman for The New York Times
There was a similar crisis of confidence in universities in the 1980s, as questions were raised about plagiarism and fabricated data in scientific research, including at Harvard. Al Gore, then a Democratic representative of Tennessee, and Representative John Dingell Jr., a Michigan Democrat, among others, held oversight hearings.
Academics argued that research misconduct was rare, and politicians contended it was underreported, according to a history published by federal agencies. Many of those testifying minimized the problem or said that criminalizing scientific fraud would create a climate of fear that would impede research.
In the current dispute, Harvard responded through a defamation lawyer when The New York Post first raised accusations of plagiarism against Dr. Gay. Mr. Ackman, writing on X, has invoked lawyers and demanded that Business Insider — which first reported the plagiarism accusations against Dr. Oxman — “suspend” its stories.
“I don’t want to say history is repeating itself, but there are shades of that,” Dr. Oransky said. Neither side, he predicted, is likely to back down. “These are really high stakes.”
Kirsten Noyes and Alain Delaquérière contributed research.
https://www.nytimes.com/2024/01/14/us/p ... 778d3e6de3
Cases involving Stanford, Harvard and M.I.T. are fueling skepticism over the thoroughness of research — even from the academic world’s biggest stars

The next big battle over higher education promises to look at plagiarism.Credit...Sophie Park for The New York Times
Marc Tessier-Lavigne, president of Stanford, resigned in August after an investigation found serious flaws in studies he had supervised going back decades.
Claudine Gay, president of Harvard, resigned as the new year dawned, under mounting accusations of plagiarism going back to her graduate student days.
Then Neri Oxman, a former star professor at M.I.T., was accused of plagiarizing from Wikipedia, among other sources, in her dissertation. Her husband, the hedge-fund billionaire Bill Ackman, was one of Dr. Gay’s most dogged critics. And he has vowed to scour the records of M.I.T.’s faculty, and its president, Sally Kornbluth, for plagiarism.
The attacks on the integrity of higher education have come fast and furious over the last few years. The federal Varsity Blues investigation, in which wealthy parents were accused of using bribery and fraud to secure spots for their children in résumé-building colleges, launched a debate over merit and the admissions game. The affirmative action lawsuit against Harvard exposed how Asian American students must perform at a higher standard to win entry. And the protests over the Israel-Hamas war opened administrators to charges that they tolerated antisemitism on their campuses.
Now the focus has moved into what may be the very soul of higher education: scholarship.
Image
Marc Tessier-Lavigne, in a blue suit, stands outside on the Stanford campus.

Marc Tessier-Lavigne, the former president of Stanford University.Credit...Carolyn Fong for The New York Times
There are differences among the cases — Dr. Tessier-Lavigne and Dr. Gay were the faces of their institutions, while Dr. Oxman is a former faculty member, who was well known in her field of computational design. Defenders of Dr. Gay and Dr. Oxman say that their lifting of words is minor, and that they were not accused of stealing ideas. And unlike Dr. Tessier-Lavigne, they have not had to retract any papers.
But the recent controversies have helped fuel the skepticism that some scholarship is not as rigorous as it purports to be.
“It does strike me that this is a problem of the universities’ own making,” said Ivan Oransky, co-founder of Retraction Watch, which keeps a database of retracted papers now numbering more than 46,000.
“They have tried every which way to avoid acknowledging just how common misconduct is in academia, and what that does is give ammunition to sometimes — let’s face it — bad-faith actors who want to undermine confidence or undermine the reputation of an institution,” Dr. Oransky said.
There is probably more to come. A congressional committee has announced that it would investigate a “hostile takeover” of higher education by “political activists, woke faculty and partisan administrators.”
A cottage industry of checking research papers had already sprung up in the last two decades, including Retraction Watch, the Center for Open Science and Data Colada, a blog dedicated to unmasking research based on bad data.
The number of retracted research papers has grown dramatically over time, to more than 10,000 retractions internationally in 2023, an annual record, according to the journal Nature, up from about 400 papers in 2010, when Retraction Watch began its work, Dr. Oransky said.
This may be in part because the scrutiny has intensified, he said. Nature also blamed the rise of paper-writing mills.
“What’s different this time is the levels at which this seems to be striking — Harvard and Stanford,” Dr. Oransky said. “These are cataclysmic events.”
Dr. Gay, a professor of government and African and African American studies, asked for a handful of corrections in citation and quotation in her dissertation and scholarly papers. But she stood by her work, and an outside panel cleared her of research misconduct.
A review panel found that Dr. Tessier-Lavigne, a neuroscientist, had not personally engaged in or known about data manipulation but that “there may have been opportunities to improve laboratory oversight and management.” He agreed to retract three papers and correct two more.
Dr. Oxman, a celebrated architect and designer, apologized on social media for some lapses in attribution in her dissertation.
Not everyone thinks academia is rife with deception.
Stephen Voss, an associate professor of political science at the University of Kentucky, said he was dismayed that in their attempts to defend Dr. Gay, some academics had suggested that plagiarism was commonplace within their ranks.
“I viewed some of these defenses of Claudine as being false confessions to misbehavior that actually is not taking place at the level her defenders wanted to suggest,” Dr. Voss said. “The ‘it goes on all the time’ argument.”
Dr. Gay is accused of copying, with only light paraphrasing, two passages from Dr. Voss’s work in her dissertation.
Dr. Voss said he was not troubled by it, since he had been her teaching fellow at Harvard, helping to teach her quantitative analysis, and later her colleague in the same lab. “It would have been quite natural for her to borrow ideas from me,” he said. “The Claudine Gay story is just going to force everybody to be a little more careful about citations.”
The internet and software like Turnitin, which targets academic publishing and research, may make it easier to detect plagiarism. And plagiarism watchers are waiting to see what the future of artificial intelligence will bring — more plagiarism or better detection?
But until now, that software has been used more against students than against professors and administrators.
Many scholars are worried that attacks on research will be used by politicians, donors and even other scholars as a pretext to go after their ideological enemies.
“A broad suspicion toward intellectuals and academics is a rich vein in American culture, and recent events have supported it,” Dr. Voss said.
Mr. Ackman, head of the hedge fund Pershing Square Capital Management, was a vocal critic of Dr. Gay’s leadership at Harvard, from her handling of antisemitism on campus to her support for diversity, equity and inclusion policies. The accusations of plagiarism against her became part of his attack.
After Dr. Gay announced that she would resign from her presidency but remain on the faculty, Mr. Ackman posted on X: “There would be nothing wrong with her staying on the faculty if she didn’t have serious plagiarism issues. Students are forced to withdraw for much less.”
Mr. Ackman declined to comment for this article.
It’s this kind of attack that concerns Jonathan Bailey, a copyright and plagiarism consultant who also runs the website Plagiarism Today. “There’s a lot of worry that the heat has been turned up and the people who are doing the evaluations don’t necessarily have academic research or journalistic integrity in mind,” he said.
Just as new accusations dribbled out against Dr. Gay until the day before she resigned, they have continued against Dr. Oxman. On Thursday, Retraction Watch posted a blog item saying that her thesis lifted about 100 words without quotation or citation from an article published in Physics World in 2000. The blog said it learned of the overlap from Steve Haake, a sports engineer who wrote the original article.
“I have never intentionally presented someone else’s words or ideas as my own,” Dr. Oxman said in a statement emailed through a spokesman for her husband on Friday, the day after the Retraction Watch item appeared. “In the process of writing a 330-page dissertation, I missed a couple of footnotes and some quotation marks. Had A.I. software been available in 2009, I could have avoided these errors. The mistakes are simply a function of my humanity.”
Even so, the attacks on academic integrity are sure to continue. “While President Gay’s resignation is welcome news, the problems at Harvard are much larger than one leader, and the committee’s oversight will continue,” said Representative Virginia Foxx, a North Carolina Republican, who heads the House Education and the Workforce Committee, after Dr. Gay’s resignation on Jan. 2.
Image
Rep. Virginia Foxx, a North Carolina Republican, sits at a table.

Representative Virginia Foxx promises to continue her investigation into higher education. Credit...Elizabeth D. Herman for The New York Times
There was a similar crisis of confidence in universities in the 1980s, as questions were raised about plagiarism and fabricated data in scientific research, including at Harvard. Al Gore, then a Democratic representative of Tennessee, and Representative John Dingell Jr., a Michigan Democrat, among others, held oversight hearings.
Academics argued that research misconduct was rare, and politicians contended it was underreported, according to a history published by federal agencies. Many of those testifying minimized the problem or said that criminalizing scientific fraud would create a climate of fear that would impede research.
In the current dispute, Harvard responded through a defamation lawyer when The New York Post first raised accusations of plagiarism against Dr. Gay. Mr. Ackman, writing on X, has invoked lawyers and demanded that Business Insider — which first reported the plagiarism accusations against Dr. Oxman — “suspend” its stories.
“I don’t want to say history is repeating itself, but there are shades of that,” Dr. Oransky said. Neither side, he predicted, is likely to back down. “These are really high stakes.”
Kirsten Noyes and Alain Delaquérière contributed research.
https://www.nytimes.com/2024/01/14/us/p ... 778d3e6de3
A Bird’s-Eye View of a Technicolor World
Scientists have devised a new video system that reveals how animals see color, and us.
Is the sky truly blue?
Video: https://vp.nyt.com/video/2024/01/17/114 ... _1080p.mp4
Forget cerulean — a bright, clear sky is actually dominated by ultraviolet light. Humans can’t see ultraviolet light, but many birds can. “Their sky will be essentially an ultraviolet sky,” said Daniel Hanley, a sensory ecologist at George Mason University
Color is in the eye of the beholder
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
The human eye contains three types of cone cells, photoreceptors that allow us to see blue, green and red light. Many animals have different combinations of photoreceptors, which means that they see the world in their own distinct color palettes. A butterfly that looks pale yellow to us might appear entirely different to an avian observer.CreditCredit...
Enter animal-vision video
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
Dr. Hanley and his colleagues have created a video camera system that creates moving representations of how other creatures see colors, such as how a spider perched on a flower might look to a honeybee. The resulting videos, which were published on Tuesday as part of a new study, give human viewers a rough animal-eye view of nature. “You actually can look at the world in new and interesting ways,” Dr. Hanley said.CreditCredit...
How a bird sees a rainbow
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
In addition to blue, green and red cone cells, many birds have cone cells that are sensitive to ultraviolet light, allowing them to see a broader spectrum of colors than people can. “Their rainbow is wider and extends lower than ours,” said Vera Vasas, a sensory ecologist at the University of Sussex in Britain and an author of the new study.CreditCredit...
How a mouse sees a rainbow
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
Mice, on the other hand, have just two types of cones — one sensitive to green and another sensitive to ultraviolet, depicted in blue in this video. To a mouse, a rainbow would be composed of two broad bands.CreditCredit...
How a bird sees a butterfly
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
When a male orange sulphur butterfly opens his wings, he will appear iridescent to birds and other animals that can see ultraviolet light. This ultraviolet iridescence is depicted here in purple. To humans, the wings would appear to be orange, yellow and black.CreditCredit...
How a honeybee sees us
Video: https://vp.nyt.com/video/2024/01/17/114 ... _1080p.mp4
Here, a human applies sunscreen. To us, sunscreen appears white because it reflects all of the wavelengths of light that are visible to the human eye. But many sunscreens are designed to absorb ultraviolet light, which is normally visible to honeybees. With little ultraviolet light escaping, the arm takes on a yellow cast in this bee-vision video.CreditCredit...
How a honeybee sees a caterpillar
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
When a black swallowtail caterpillar feels threatened, it may display a V-shaped defensive gland known as the osmeterium. To the human eye, the osmeterium would appear yellow. But to honeybees, it would be an eye-catching ultraviolet, depicted here as magenta. (The gland would also appear ultraviolet to many of the birds that prey on the caterpillars.)CreditCredit...
Exploring the world in living color
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
The new video tool can capture natural, real-world behavior, revealing, for instance, how bees might look to one another as they forage or interact. Color cues can change quickly over time and as animals change position, the researchers noted. “To prove that the system works, I have learned things that I didn’t know,” Dr. Vasas said. “And I am supposed to be a color vision expert!”
Produced by Antonio de Luca
The study was published in PLOS Biology on Tuesday, Jan 23. Details are available here https://journals.plos.org/plosbiology/a ... io.3002444 .
https://www.nytimes.com/2024/01/23/scie ... 778d3e6de3
Video
Is the sky truly blue?
Video: https://vp.nyt.com/video/2024/01/17/114 ... _1080p.mp4
Forget cerulean — a bright, clear sky is actually dominated by ultraviolet light. Humans can’t see ultraviolet light, but many birds can. “Their sky will be essentially an ultraviolet sky,” said Daniel Hanley, a sensory ecologist at George Mason University
Color is in the eye of the beholder
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
The human eye contains three types of cone cells, photoreceptors that allow us to see blue, green and red light. Many animals have different combinations of photoreceptors, which means that they see the world in their own distinct color palettes. A butterfly that looks pale yellow to us might appear entirely different to an avian observer.CreditCredit...
Enter animal-vision video
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
Dr. Hanley and his colleagues have created a video camera system that creates moving representations of how other creatures see colors, such as how a spider perched on a flower might look to a honeybee. The resulting videos, which were published on Tuesday as part of a new study, give human viewers a rough animal-eye view of nature. “You actually can look at the world in new and interesting ways,” Dr. Hanley said.CreditCredit...
How a bird sees a rainbow
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
In addition to blue, green and red cone cells, many birds have cone cells that are sensitive to ultraviolet light, allowing them to see a broader spectrum of colors than people can. “Their rainbow is wider and extends lower than ours,” said Vera Vasas, a sensory ecologist at the University of Sussex in Britain and an author of the new study.CreditCredit...
How a mouse sees a rainbow
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
Mice, on the other hand, have just two types of cones — one sensitive to green and another sensitive to ultraviolet, depicted in blue in this video. To a mouse, a rainbow would be composed of two broad bands.CreditCredit...
How a bird sees a butterfly
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
When a male orange sulphur butterfly opens his wings, he will appear iridescent to birds and other animals that can see ultraviolet light. This ultraviolet iridescence is depicted here in purple. To humans, the wings would appear to be orange, yellow and black.CreditCredit...
How a honeybee sees us
Video: https://vp.nyt.com/video/2024/01/17/114 ... _1080p.mp4
Here, a human applies sunscreen. To us, sunscreen appears white because it reflects all of the wavelengths of light that are visible to the human eye. But many sunscreens are designed to absorb ultraviolet light, which is normally visible to honeybees. With little ultraviolet light escaping, the arm takes on a yellow cast in this bee-vision video.CreditCredit...
How a honeybee sees a caterpillar
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
When a black swallowtail caterpillar feels threatened, it may display a V-shaped defensive gland known as the osmeterium. To the human eye, the osmeterium would appear yellow. But to honeybees, it would be an eye-catching ultraviolet, depicted here as magenta. (The gland would also appear ultraviolet to many of the birds that prey on the caterpillars.)CreditCredit...
Exploring the world in living color
Video: https://vp.nyt.com/video/2024/01/21/114 ... _1080p.mp4
The new video tool can capture natural, real-world behavior, revealing, for instance, how bees might look to one another as they forage or interact. Color cues can change quickly over time and as animals change position, the researchers noted. “To prove that the system works, I have learned things that I didn’t know,” Dr. Vasas said. “And I am supposed to be a color vision expert!”
Produced by Antonio de Luca
The study was published in PLOS Biology on Tuesday, Jan 23. Details are available here https://journals.plos.org/plosbiology/a ... io.3002444 .
https://www.nytimes.com/2024/01/23/scie ... 778d3e6de3
Video
Re: Concept of Knowledge Revisited
Higher Education Needs More Socrates and Plato

By Ezekiel J. Emanuel and Harun Küçük
Dr. Emanuel and Dr. Küçük are on the faculty of the University of Pennsylvania, where Dr. Emanuel is a professor and the vice provost for global initiatives and Dr. Küçük is an associate professor of the history and sociology of science.
The right attacks colleges and universities as leftist and woke. Progressives castigate them as perpetuating patriarchy and white privilege. The burdens of these culture war assaults are compounded by parents worried that the exorbitant costs of higher education aren’t worth it.
No wonder Americans’ faith in universities is at a low. Only 36 percent of Americans have confidence in higher education, according to a survey by Gallup last year, a significant drop from eight years ago. And this was before colleges and universities across the country were swept up in a wave of protests and counter-protests over the war in Gaza.
But the problems facing American higher education are not just the protests and culture war attacks on diversity, course content, speech and speakers. The problem is that higher education is fundamentally misunderstood. In response, colleges and universities must reassert the liberal arts ideals that have made them great but that have been slipping away.
By liberal arts, we mean a broad-based education that aspires to send out into society an educated citizenry prepared to make its way responsibly in an ever-more complex and divided world. We worry that at many schools, students can fulfill all or most of their general education requirements and take any number of electives without having had a single meaningful discussion that is relevant to one’s political life as a citizen.
Over the past century, what made American higher education the best in the world is not its superiority in career training, but educating students for democratic citizenship, cultivating critical thinking and contributing to the personal growth of its students through self-creation. To revive American higher education, we need to reinvigorate these roots.
In Europe and many countries elsewhere, colleges and universities have undergraduates specialize from Day 1, focusing on developing area-specific skills and knowledge. College students are trained to become doctors, lawyers or experts in international relations, English literature or computer science.
In the United States, European-style specialization for medical, legal, business or public policy careers is the purpose of post-collegiate professional schools. Traditionally, the American college has been about imparting a liberal arts education, emphasizing reasoning and problem solving. Those enduring skills are the critical ingredients for flourishing companies and countries.
Historically, students arriving on American college campuses spent a majority of their first two years taking classes outside their projected majors. This exposed them to a common curriculum that had them engage with thoughtful writings of the past to develop the skills and capacity to form sound, independent judgments.
Over the past half century, American colleges and universities have moved away from this ideal, becoming less confident in their ability to educate students for democratic citizenship. This has led to a decline in their commitment to the liberal arts, a trend underscored in the results last year of a survey of chief academic officers at American colleges and universities by Inside Higher Ed. Nearly two-thirds agreed that liberal arts education was in decline, and well over half felt that politicians, college presidents and university boards were increasingly unsympathetic to the liberal arts.
Today, there is almost no emphasis on shared courses among majors that explore and debate big questions about the meaning of equality, justice, patriotism, personal obligations, civic responsibility and the purpose of a human life. Majors that once required only eight or 10 courses now require 14 or more, and students are increasingly double majoring — all of which crowds out a liberal arts education. Ambitious students eager to land a prestigious consulting, finance or tech job will find it too easy to brush aside courses in the arts, humanities and social and natural sciences — the core of a liberal education.
The devaluing of the first two years of a shared liberal arts education has shortchanged our students and our nation. Educating young adults to be citizens is why the first two years of college still matter.
To that end, the so-called Great Books have long been the preferred way to foster citizenship. This approach is not, contrary to critics on the left and right, about sanctifying specific texts for veneration or a mechanism for heritage transmission.
Books by Plato, Aristotle, Hobbes, Locke, Kant, Emerson, Thoreau, Whitman as well as Wollstonecraft, Austen, Woolf, Baldwin, Hurston and Orwell are worthy of introductory collegiate courses for students of all majors. These writers address the fundamental questions of human life. They explore the ideas of self-determination, friendship, virtue, equality, democracy and religious toleration and race that we have all been shaped by.
As students address those big questions, the Great Books authors provide a road map as they challenge and criticize one another and the conventional wisdom of the past. The Socrates of Plato’s dialogues is the exemplar — asking about beliefs and then subjecting them to respectful but critical analysis and skepticism.
These books are best studied in small seminar discussions, which model and inculcate in students democratic behavior. This discourse is an antidote to the grandstanding in today’s media and social media.
The teacher is less an expert in specific writers and more a role model for intellectual curiosity, asking probing questions, offering critical analyses and seeking deeper understanding. In an idealized Socratic fashion, these discussions require listening at length and speaking briefly and, most important, being willing to go where the argument leads.
Parents who are paying for college might question the value of spending $80,000 a year so that their son or daughter can read Plato, Hobbes and Thoreau instead of studying molecular biology or machine learning. But discussing life’s big value questions in seminars gives students personal engagement with professors that can never be reproduced in large lecture halls. Discussions among students on their deepest thoughts cultivates curiosity and empathy, and forges bonds of friendship important for citizenship and fulfilling lives.
Although we like to set ourselves apart from the past by appeals to modernity, the fundamental questions that we find ourselves asking are not always modern, and the latest answer is not always right. But how would you know how to think beyond the readily presented check boxes if you haven’t done the work of laying things out and putting them back together for yourself?
War was no less a concern for Thucydides, Tacitus and Thoreau than it is today. Discussing Great Books allows students to gain distance from the daily noise and allows their reason to roam free among principles and foundations rather than becoming absorbed in contemporary events. Our biggest problems are often best addressed not by leaning in but by stepping away to reflect on enduring perspectives.
Liberal arts education is not value neutral. That is why it is indispensable today. Freedom of thought, critical reasoning, empathy for others and respectful disagreement are paramount for a flourishing democratic society. Without them, we get the unreasoned condemnations so pervasive in today’s malignant public discourse. With them, we have a hope of furthering the shared governance that is vital to America’s pluralistic society.
https://www.nytimes.com/2024/05/19/opin ... 778d3e6de3

By Ezekiel J. Emanuel and Harun Küçük
Dr. Emanuel and Dr. Küçük are on the faculty of the University of Pennsylvania, where Dr. Emanuel is a professor and the vice provost for global initiatives and Dr. Küçük is an associate professor of the history and sociology of science.
The right attacks colleges and universities as leftist and woke. Progressives castigate them as perpetuating patriarchy and white privilege. The burdens of these culture war assaults are compounded by parents worried that the exorbitant costs of higher education aren’t worth it.
No wonder Americans’ faith in universities is at a low. Only 36 percent of Americans have confidence in higher education, according to a survey by Gallup last year, a significant drop from eight years ago. And this was before colleges and universities across the country were swept up in a wave of protests and counter-protests over the war in Gaza.
But the problems facing American higher education are not just the protests and culture war attacks on diversity, course content, speech and speakers. The problem is that higher education is fundamentally misunderstood. In response, colleges and universities must reassert the liberal arts ideals that have made them great but that have been slipping away.
By liberal arts, we mean a broad-based education that aspires to send out into society an educated citizenry prepared to make its way responsibly in an ever-more complex and divided world. We worry that at many schools, students can fulfill all or most of their general education requirements and take any number of electives without having had a single meaningful discussion that is relevant to one’s political life as a citizen.
Over the past century, what made American higher education the best in the world is not its superiority in career training, but educating students for democratic citizenship, cultivating critical thinking and contributing to the personal growth of its students through self-creation. To revive American higher education, we need to reinvigorate these roots.
In Europe and many countries elsewhere, colleges and universities have undergraduates specialize from Day 1, focusing on developing area-specific skills and knowledge. College students are trained to become doctors, lawyers or experts in international relations, English literature or computer science.
In the United States, European-style specialization for medical, legal, business or public policy careers is the purpose of post-collegiate professional schools. Traditionally, the American college has been about imparting a liberal arts education, emphasizing reasoning and problem solving. Those enduring skills are the critical ingredients for flourishing companies and countries.
Historically, students arriving on American college campuses spent a majority of their first two years taking classes outside their projected majors. This exposed them to a common curriculum that had them engage with thoughtful writings of the past to develop the skills and capacity to form sound, independent judgments.
Over the past half century, American colleges and universities have moved away from this ideal, becoming less confident in their ability to educate students for democratic citizenship. This has led to a decline in their commitment to the liberal arts, a trend underscored in the results last year of a survey of chief academic officers at American colleges and universities by Inside Higher Ed. Nearly two-thirds agreed that liberal arts education was in decline, and well over half felt that politicians, college presidents and university boards were increasingly unsympathetic to the liberal arts.
Today, there is almost no emphasis on shared courses among majors that explore and debate big questions about the meaning of equality, justice, patriotism, personal obligations, civic responsibility and the purpose of a human life. Majors that once required only eight or 10 courses now require 14 or more, and students are increasingly double majoring — all of which crowds out a liberal arts education. Ambitious students eager to land a prestigious consulting, finance or tech job will find it too easy to brush aside courses in the arts, humanities and social and natural sciences — the core of a liberal education.
The devaluing of the first two years of a shared liberal arts education has shortchanged our students and our nation. Educating young adults to be citizens is why the first two years of college still matter.
To that end, the so-called Great Books have long been the preferred way to foster citizenship. This approach is not, contrary to critics on the left and right, about sanctifying specific texts for veneration or a mechanism for heritage transmission.
Books by Plato, Aristotle, Hobbes, Locke, Kant, Emerson, Thoreau, Whitman as well as Wollstonecraft, Austen, Woolf, Baldwin, Hurston and Orwell are worthy of introductory collegiate courses for students of all majors. These writers address the fundamental questions of human life. They explore the ideas of self-determination, friendship, virtue, equality, democracy and religious toleration and race that we have all been shaped by.
As students address those big questions, the Great Books authors provide a road map as they challenge and criticize one another and the conventional wisdom of the past. The Socrates of Plato’s dialogues is the exemplar — asking about beliefs and then subjecting them to respectful but critical analysis and skepticism.
These books are best studied in small seminar discussions, which model and inculcate in students democratic behavior. This discourse is an antidote to the grandstanding in today’s media and social media.
The teacher is less an expert in specific writers and more a role model for intellectual curiosity, asking probing questions, offering critical analyses and seeking deeper understanding. In an idealized Socratic fashion, these discussions require listening at length and speaking briefly and, most important, being willing to go where the argument leads.
Parents who are paying for college might question the value of spending $80,000 a year so that their son or daughter can read Plato, Hobbes and Thoreau instead of studying molecular biology or machine learning. But discussing life’s big value questions in seminars gives students personal engagement with professors that can never be reproduced in large lecture halls. Discussions among students on their deepest thoughts cultivates curiosity and empathy, and forges bonds of friendship important for citizenship and fulfilling lives.
Although we like to set ourselves apart from the past by appeals to modernity, the fundamental questions that we find ourselves asking are not always modern, and the latest answer is not always right. But how would you know how to think beyond the readily presented check boxes if you haven’t done the work of laying things out and putting them back together for yourself?
War was no less a concern for Thucydides, Tacitus and Thoreau than it is today. Discussing Great Books allows students to gain distance from the daily noise and allows their reason to roam free among principles and foundations rather than becoming absorbed in contemporary events. Our biggest problems are often best addressed not by leaning in but by stepping away to reflect on enduring perspectives.
Liberal arts education is not value neutral. That is why it is indispensable today. Freedom of thought, critical reasoning, empathy for others and respectful disagreement are paramount for a flourishing democratic society. Without them, we get the unreasoned condemnations so pervasive in today’s malignant public discourse. With them, we have a hope of furthering the shared governance that is vital to America’s pluralistic society.
https://www.nytimes.com/2024/05/19/opin ... 778d3e6de3